You don’t realise how important it is to get your critical spares holding right until your $50K/hr machine is sitting dead with an emergency part all the way in a different city.
So how does your warehouse ensure you have what you need, when you need it? Who decides how much to stock?
Well… in most cases on mining sites there is no real math behind this number, and that’s a shame considering how much not having spares costs us in lost opportunity.
In this article we will show you have to calculate the optimal level of spares holding for a required level of availability, in Excel using the Poisson distribution.
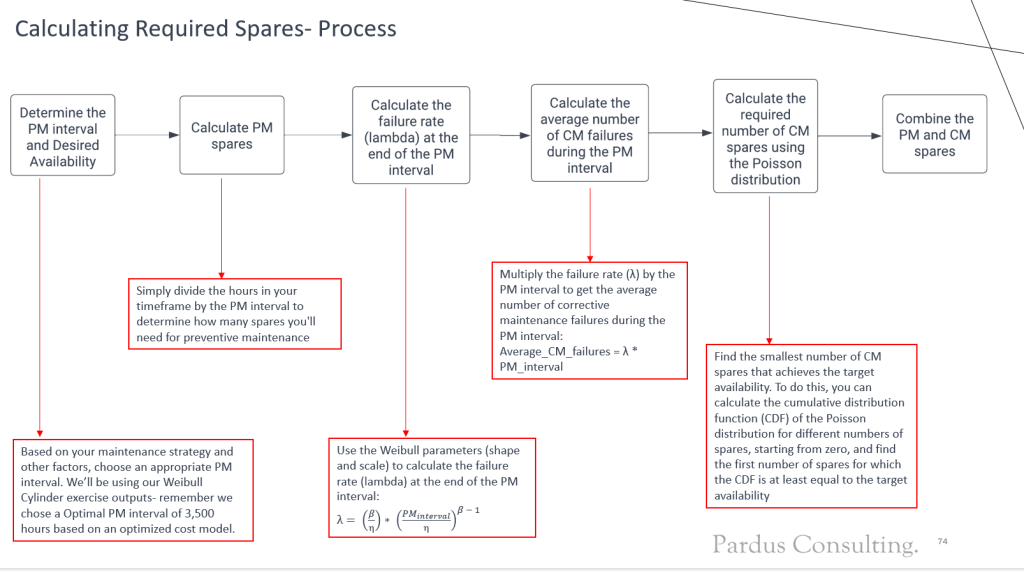
Before starting Step 1, it’s important to understand why the Poisson distribution is chosen for modeling spares. It is ideal for estimating required spares due to its ability to accurately represent the random occurrence of equipment failures and the resulting demand for spare parts. In this article’s model, we’ll calculate the failure rate for a chosen maintenance interval, determining the risk of needing corrective maintenance within that period.
This calculation helps in estimating the necessary corrective maintenance spares, upon which we use the Poisson distribution to ascertain the required spares for maintaining a specific level of availability.
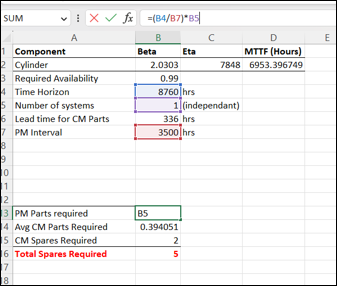
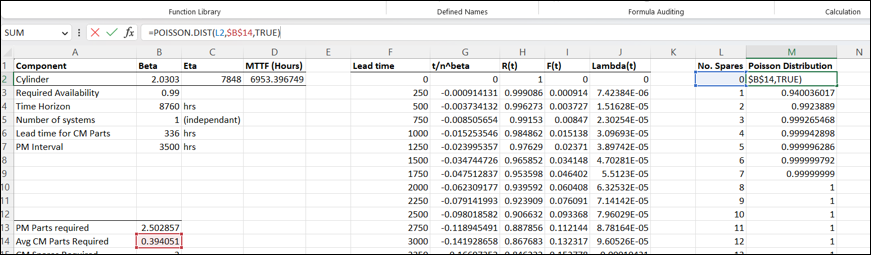
The table above provides essential data for creating the Spares model, incorporating Beta and Eta values from prior Weibull Analysis for Lambda (failure rate) calculation, targeting 99% spares availability over a 8760-hour annual operation period. The model’s output determines the annual spares requirement. Additionally, a Preventative Maintenance (PM) Interval of 3500 hours has been set for servicing the cylinders.
For the first step in calculating the optimal spares level, we must calculate the required spares for Preventative Maintenance (PM). This is the easiest calculation because if I plan to replace a cylinder every 3500 hours, I will plan to replace 8760/3500 = 2.5 cylinders per year. In reality this can be rounded to 3 because we can’t have half-spares, but because we’re adding the Corrective Maintenance spares allowance on later, we will keep this value exact so that the final number is more in-line with the risk profile.
Next, we will calculate the failure rate from our Beta and Eta values to quantify the risk of failing a part with an increase in maintenance interval. We’ve covered this calculation in depth in the Weibull Analysis article, however the formula to use is:
\[\lambda = (\frac) \times (\frac)^{(\beta -1)}\]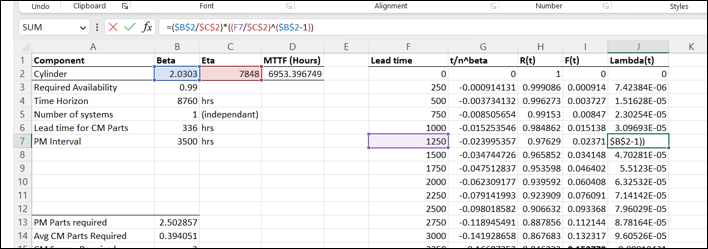
After having calculated our failure rate for each PM interval, we can highlight the 3500 hours row we initially determined as the interval we will be doing replacements. What is obvious is that as I increase my replacement interval, the risk of failure or Lambda will increase. To convert this to a tangible number of spares we just multiply the failure rate by the PM hours, 3500. Note this takes into account a single component system (so 1 cylinder).
\[CM Spares = \lambda \times PM Interval\]In this example it comes out to about 0.3 of a spare part (again, don’t round this out to 1 just yet). This is known as the mean for the CM spares, and will be important in our next and final step.
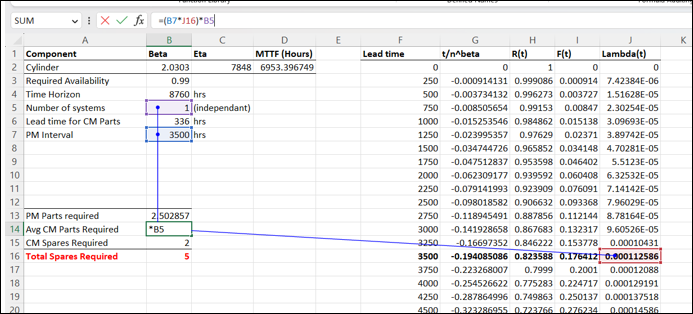
Now that we have a number for the required PM and mean CM spares, we need to adjust the mean CM spares number for the required availability we specified at the start (99%).
We use the Poisson distribution formula in excel where we fill in the number of required spares in increasing order, the mean CM Spares value, and TRUE- because we went a cumulative number for part availability. When we drag this formula down you will see that as I increase my spares holding, my part availability increases- logical.
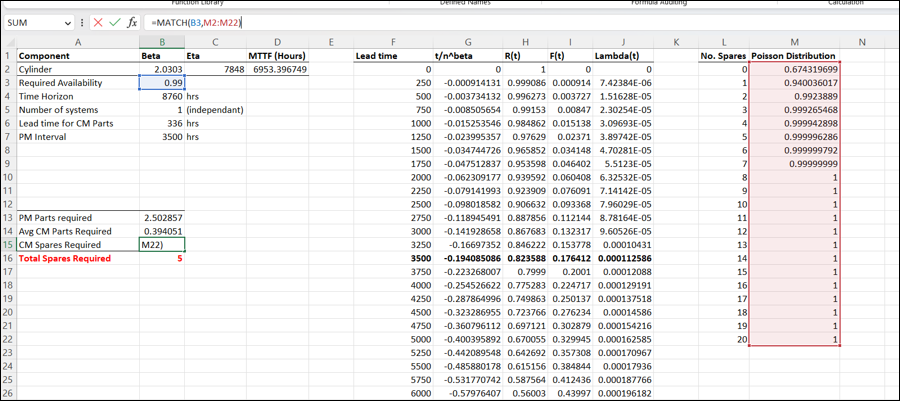
What we then do is match the Poisson distribution values of availability to our 99% and select the corresponding number of CM spares using the MATCH function. We then add this number to our required PM parts and now we round up using the CEIL function. This now calculated we should hold 5 spares continuously to ensure we have sufficient parts available for preventative services and breakdowns. This number ensures we will have a cylinder in stock 99% of the time.
As you can see, calculating the required spares for a certain level of part availability isn’t technically arduous, however it is important to note a few caveats- namely that if the Beta and Eta values from your Weibull analysis are wrong, the spares will be way off as well.
You must also keep in mind that this calculation doesn’t take into account the lead time of the part from the manufacturer to your site, so the economic order qty and optimum stock level must also be calculated, however this is usually built into stores management software and falls outside the realm of the Reliability Engineer. This calculation shows how much you should have on-hand to ensure a part will be available when you need it, but if lead times are large, this number will increase as it needs to keep a minimum of 5 as in this example.
And finally, be realistic with the required part availability, as stock holding costs and space increase dramatically when you require a high level of part availability- this is also a cost optimization problem, which isn’t covered here, but follows the same principle as calculating optimal maintenance intervals covered in an earlier article. We don’t always require 99% part availability, and you’ll see that even in the above calculation, you can achieve 94% availability with only 1 CM spare, which may be enough in your case.
Original Article: Pardus Consulting Australia
Leave a Reply