
There is something very powerful about working in teams. That power becomes evident when you look at teams as human structures built to deliver reliable outcomes. Managers who want higher reliability, top quality production and fewer problems need to understand why teams are so powerful and how to gain that power for themselves.
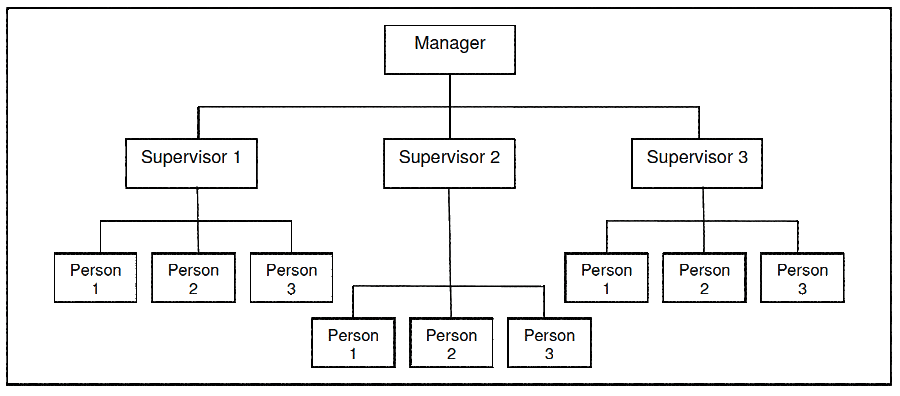
The typical organisational hierarchy structure shown in Figure 1 is common for organisations. That structure developed from fighting battles and wars. It is a poor structure for helping companies to achieve their goals, because it requires managers to the make decisions alone, often hurriedly. It is a high risk design for long-term business success. It encourages managers’ egos and ambitions to drive their decisions, rather than making decisions based on careful analysis and understanding of a situation. It promotes human conflict because the person at the top has final authority, yet that person maybe incompetent, ignorant or ill. The hierarchy organisation design does not encourage good business decisions. It has had its day in those organisations that want top quality products, high equipment reliability and world-class production.
In the mid to late Twentieth Century, it became impossible for one person to know all that was necessary to do a job well. The amount of knowledge became too great for a person to handle. That is even more the case today. One structure that can address this situation of vast information requirements to make good business decisions is teams of subject-matter experts working together in teamwork. Teams are a quality and reliability improvement tool and a risk control device. A well-functioning team will automatically produce better results and reduce production problems. This explains why autonomous work teams are such a popular concept. These teams solve problems and prevent problems because they have the ability to analyse and resolve issues as a team of subject-matter experts. They learn what to do and pass that learning throughout the whole team.
There is a scientific reason why teams improve the chance of success. A team-based decision-cell structure is mathematical a better design for a business then the militaristic hierarchy structure. Group decisions are more likely to be better choices. The science and maths of probability and reliability allow deep insights into why and how teams can get better outcomes, and especially why they are a powerful structure for achieving business goals.
To understand the science of how teams and teamwork provide improved quality, reliability and risk control, it is necessary to understand first how organisations get work done. All work is a series of actions done one after the other. The sequence of actions makes up tasks. The accumulated tasks make up jobs. This forms a series process. Figure 2, shows a 5-task job that produces a wanted output. Each task has a chance of success between zero and 100%. Figure 3 shows within each task there are activities. These also form a series arrangement.

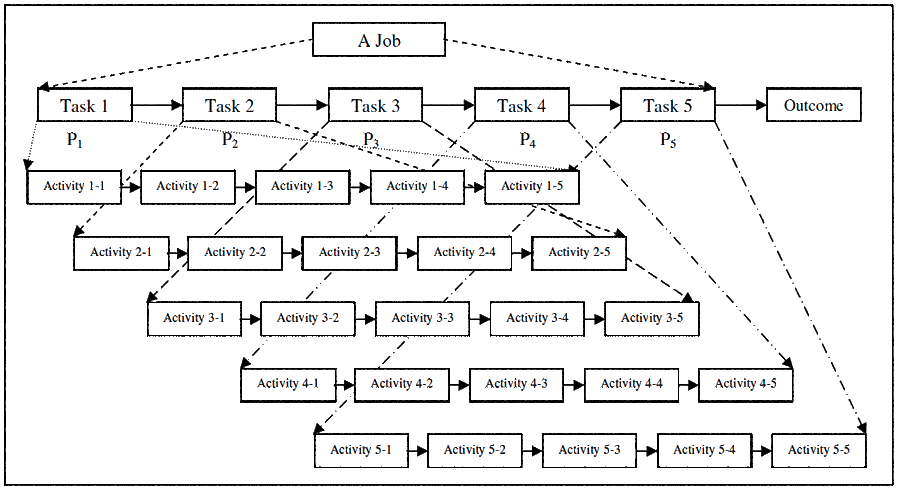
When you have a series of activities following each other, where the next activity builds on the work performed by the previous ones, it only requires one error to happen and the whole job goes wrong. To get the right outcome the first time in Figure 3 requires 25 activities be done perfectly. If only one activity in one task is wrong, the outcome will be wrong. The job will be scrap. What is the chance that each activity will be done right, and the whole job will be 100% right?
To calculate the chance that the whole job will be right, we first must know the chance of doing each task right. There is data available on human error rates for doing tasks1. The error rate depends on the difficulty of the task and the stress of the situation. Hard tasks, not often done, have higher error rates. Add stress to the situation and the failure rate gets even worse.
For complicated maintenance and operating activities, error rates of 10%, or 1 error in 10 opportunities, are common. Once we know the error rate of a task is 10%, we know the chance it will be right is 90%. For the sake of the example, let us say that each of the tasks in Figure 2 have a 90% chance of being done right. Once we know that, we can calculate the chance of the whole job being right by using the simple probability formula (chance is another name for it):
Pseries= P1 x P2 x P3 x …Pn
The formula says the chance for the whole series is the multiplication of the individual task chances. Assuming a 90% chance for each task in our job of being right, we can use the formula to work-out the chance for the whole job going right.
Pseries = 0.9 x 0.9 x 0.9 x 0.9 x 0.9
= 0.59 or 59%
The formula says that we have a 59% chance the whole job will be perfectly right every time it is done. From a 90% chance of each task being correct, we have got a 59% chance the job will be correct. About 4 times out of every 10 times the job is done, it will be wrong.
If we want our job to be right-first-time, 99% of the time, we would need to guarantee that each task is right 99.8% of the time. In other words, if we want the job to be right 99 times out of 100, each task must be right 998 times out of 1000. We have to be much more careful in doing each task, if we want top outcomes at the end of the job.
Because most of the work done in the world is a series process, the mathematics of chance warn us that unless we have good results at every step, many of our jobs will go wrong and need to be scrapped or repeated. You need to control chance if you want to stop waste and loss. You need to ensure good things happen in all our tasks so that you get great results at the end of the job.
What has chance got to do with teams and team work? Figure 4 is a simple illustration of what happens in well-functioning teams. The people in the team work-off each other. When a person is uncertain about a decision, they ask other team members for advice. If the team is a mix of subject matter experts, then each is a knowledgeable resource that the others use to help them do better work.
An example might be an autonomous work team of operators, maintainers and quality control staff in a production department. The maintainer can advise the other team members on equipment reliability issues, the operator has experience in using the production equipment and the quality control people can advise on product performance. Each member contributes their best advice and experience to the decision making processes of every other team member. Instead of having one person working alone, with a team there are several people helping each other to do their work. This interaction improves the chance that things will go right more often for everyone on the team.
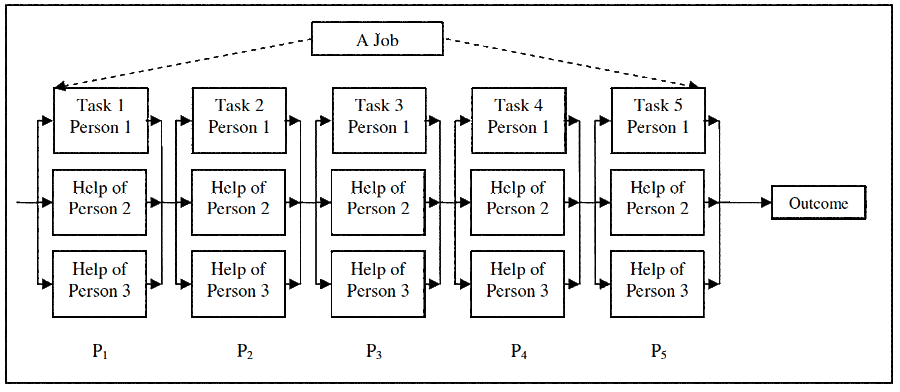
How much difference does a well-functioning team make to the chance of a job going right? Figure 5 shows the 5-task job, as a team would do it, with everyone helping other team members to get the best result. In Figure 5, Person 1 is doing the work, with the support from two others on the team. Each person adds his or her useful contribution at each step. The arrangement of each task is now a parallel activity. This arrangement also has a mathematical formula to work-out the chance that a task will be right.
The formula is:
Pparallel = 1 – [(1-P1) x (1-P2) x ….(1-Pn)]
We do not need the formula to see that each task now has three people watching it. If one person gets it wrong, there are two others checking them. Hopefully one of them will notice it is wrong and correct it. If we were to use the equation, we would find that with three people, each having 90% chance of accuracy, the parallel combination gives us a task that is right 99.9% of the time, and the job is right 99.5% of the time.
By paralleling the tasks with a team, we have gone from 59% chance of the job being right when a person works alone, to 99.9% with a team of subject matter experts working together. That is why teams are so powerful. Once people parallel-up in well functioning teams to help each other, the odds of getting better results jump sky-high.
Another example of a parallel process is the old carpenter’s advice, ‘Measure twice, and cut once’. The carpenter knows that the double-check will save problems and trouble later. We can turn the adage into a simple parallel process, as in Figure 6.

The typical error rate in reading a tape measure is five times in every thousand you will misread it, or 995 times out of 1000, it will be right. Without the parallel task, the carpenter will cut the wood in the wrong spot about once every 200 times. It is not hard to imagine a carpenter doing 50 cuts a day. So about once a working week, they would cut the wood wrong and have to throw it away.
With the second test ‘measure’ added, the chance of getting the cut right rises to 99.998% and the error rate falls to twice in every 10,000 times. With 50 cuts a day, they will make an error once every 100 working days, or about once every 20 working weeks. Can you now see the power of parallelling test activities to every task, and ensuring that they are right? For our carpenter the simple addition of a check test produced twenty times fewer mistakes.
Teams bring this power to organisations. Teams can get people checking each other so that everyone improves their chance of doing outstanding work. They have the ability to improve greatly the chance of delivering right-first-time results. Teams and teamwork are the way to go in those companies that want high quality, high reliability and fewer risks. Maybe it is time you look at changing your organisation structure to one that is team based – the numbers are in your favour!
My best regards to you,
Mike Sondalini
1 Smith, J. David, ‘Reliability, Maintability and Risk’, Elsevier,7th Edition, Appendix 6
 Ask a question or send along a comment.
Please login to view and use the contact form.
Ask a question or send along a comment.
Please login to view and use the contact form.
Leave a Reply