Why are Weibull, lognormal, and exponential distributions more appropriate than others for modeling failure distributions?
In this article, I want to show you why Weibull, lognormal, and exponential distributions are more appropriate than others for modeling failure distributions. Instead of starting from the explanation of the most used fitting distributions in reliability engineering, I will begin with the analysis of artificial datasets created assuming specific failure behaviors. In other words, I will start from the data and not from the statistical distributions. I think that this approach can help those who deal with this topic for the first time.
Before delving into the topic let’s recall the concept of failure rate and failure probability. These two quantities will be used when elaborating the artificial datasets.
Failure rate is defined as the number of failures in a certain time interval (eq.1)
$$ \lambda(t)=(n(t)-\frac{n(t+\delta t))}{(\delta t\centerdot n(t))} \tag{eq1} $$
Where:
- $-n(t)-$: number of operational units at time t.
- $- \delta t -$: time interval
The numerator $-n(t) – n(t + \delta t)-$ represents the number of failures occurred in the time interval $- \delta t -$.
Failure probability is defined as the probability that an item fails after a certain time (eq.2).
$$ R(t)=\frac{n(t)}{n_{0}} \tag{eq2} $$
Where:
- $-n_{0}-$: number of operational units at time t = 0.
In the following I’m going to show four different examples of datasets, They are created assuming different failure behaviors. In all the examples, the number of samples at the beginning of the analysis is n = 10.000 and a unitary time frame is used.
Example 1 – constant failure rate.
For the dataset of failures in Table 1 I’ve assumed a constant failure rate: λ = 0.1.
Table 1. Example 1: constant failure rate. λ = 0.1; Inputs:
| Survival at the beginning of the time interval | Failure rate | Failures | Time interval | Failures (cumulated) | Failure probability |
| 10000 | 0.1 | 1000 | 1 | 1000 | 0.10 |
| 9000 | 0.1 | 900 | 2 | 1900 | 0.19 |
| 8100 | 0.1 | 810 | 3 | 2710 | 0.27 |
| 7290 | 0.1 | 729 | 4 | 3439 | 0.34 |
| 6561 | 0.1 | 656 | 5 | 4095 | 0.41 |
| 5905 | 0.1 | 590 | 6 | 4686 | 0.47 |
| 5314 | 0.1 | 531 | 7 | 5217 | 0.52 |
| 4783 | 0.1 | 478 | 8 | 5695 | 0.57 |
| 4305 | 0.1 | 430 | 9 | 6126 | 0.61 |
| 3874 | 0.1 | 387 | 10 | 6513 | 0.65 |
| 3487 | 0.1 | 349 | 11 | 6862 | 0.69 |
| 3138 | 0.1 | 314 | 12 | 7176 | 0.72 |
| 2824 | 0.1 | 282 | 13 | 7458 | 0.75 |
| 2542 | 0.1 | 254 | 14 | 7712 | 0.77 |
| 2288 | 0.1 | 229 | 15 | 7941 | 0.79 |
| 2059 | 0.1 | 206 | 16 | 8147 | 0.81 |
| 1853 | 0.1 | 185 | 17 | 8332 | 0.83 |
| 1668 | 0.1 | 167 | 18 | 8499 | 0.85 |
| 1501 | 0.1 | 150 | 19 | 8649 | 0.86 |
| 1351 | 0.1 | 135 | 20 | 8784 | 0.88 |
| 1216 | 0.1 | 122 | 21 | 8906 | 0.89 |
A constant failure rate implies that in each time interval the quotient between the number of failures at the end of the time interval and the surviving items at the beginning of the time interval is constant (Figure 1a). Does the assumption of constant failure rate apply to any failure-related event? Yes, if failure is caused by random phenomena. Examples are: flat tire due to a sharp object, electronics failure due to power surge, electronics failure due to cosmic radiation. In these cases, the failure rate doesn’t change with time. In more simple words, the failure rate related to a flat tire due to a sharp object does not depend on the tire age.
Figure 1b shows the number of failures over time. Data points shown in Figure 1b can be well fitted by an exponential distribution. Alternatively, the Weibull distribution with shape parameter β = 1 can be applied.
Example 2 – linearly increasing failure rate.
For the dataset in Table 2, I’ve assumed a linearly increasing failure rate (λi+1 = λi + 0.04; λ0 = 0.04).
Table 2. Example 2: increasing failure rate: λi+1 = λi + 0.04; λ0 = 0.04.
| Survival at the beginning of the time interval | Failure rate | Failures | Time interval | Failures (cumulated) | Failure probability |
| 10000 | 0.04 | 400 | 1 | 400 | 0.04 |
| 9600 | 0.08 | 768 | 2 | 1168 | 0.12 |
| 8832 | 0.12 | 1060 | 3 | 2228 | 0.22 |
| 7772 | 0.16 | 1244 | 4 | 3471 | 0.35 |
| 6529 | 0.20 | 1306 | 5 | 4777 | 0.48 |
| 5223 | 0.24 | 1253 | 6 | 6031 | 0.60 |
| 3969 | 0.28 | 1111 | 7 | 7142 | 0.71 |
| 2858 | 0.32 | 915 | 8 | 8057 | 0.81 |
| 1943 | 0.36 | 700 | 9 | 8756 | 0.88 |
| 1244 | 0.40 | 498 | 10 | 9254 | 0.93 |
| 746 | 0.44 | 328 | 11 | 9582 | 0.96 |
| 418 | 0.48 | 201 | 12 | 9783 | 0.98 |
| 217 | 0.52 | 113 | 13 | 9896 | 0.99 |
| 104 | 0.56 | 58 | 14 | 9954 | 1.00 |
| 46 | 0.60 | 28 | 15 | 9982 | 1.00 |
| 18 | 0.64 | 12 | 16 | 9993 | 1.00 |
| 7 | 0.68 | 4 | 17 | 9998 | 1.00 |
| 2 | 0.72 | 2 | 18 | 9999 | 1.00 |
| 1 | 0.76 | 0 | 19 | 10000 | 1.00 |
| 0 | 0.80 | 0 | 20 | 10000 | 1.00 |
Does this assumption apply to any failure-related event? Yes, if failure is caused by wear-out mechanisms. Wear-out mechanisms are time dependent. That means the older the product, the higher the number of failures for the same time interval will be. Examples of wear-out mechanisms are: fatigue, wear, creep, thermal ageing. Plotting failures over time results in a different shape when compared to example 1 (Figure 2b). Failures initially increase but with decreasing number of alive items they start to decrease until all items have failed.
In this case, positively skewed distributions such as Weibull or lognormal distribution can be used for fitting failures.
Example 3 – linearly decreasing failure rate.
For the dataset in Table 3, I’ve assumed a linearly decreasing failure rate (λi+1 = λi – 0.01; λ0 = 0.05).
Table 3. Example 3: linearly decreasing failure rate: λi+1 = λi – 0.01; λ0 = 0.05.
| Survival at the beginning of the time interval | Failure rate | Failures | Time interval | Failures (cumulated) | Failure probability |
| 10000 | 0.050 | 500 | 1 | 500 | 0.05 |
| 9500 | 0.049 | 466 | 2 | 966 | 0.10 |
| 9035 | 0.048 | 434 | 3 | 1399 | 0.14 |
| 8601 | 0.047 | 404 | 4 | 1803 | 0.18 |
| 8197 | 0.046 | 377 | 5 | 2180 | 0.22 |
| 7820 | 0.045 | 352 | 6 | 2532 | 0.25 |
| 7468 | 0.044 | 329 | 7 | 2861 | 0.29 |
| 7139 | 0.043 | 307 | 8 | 3168 | 0.32 |
| 6832 | 0.042 | 287 | 9 | 3455 | 0.35 |
| 6545 | 0.041 | 268 | 10 | 3723 | 0.37 |
| 6277 | 0.040 | 251 | 11 | 3974 | 0.40 |
| 6026 | 0.039 | 235 | 12 | 4209 | 0.42 |
| 5791 | 0.038 | 220 | 13 | 4429 | 0.44 |
| 5571 | 0.037 | 206 | 14 | 4635 | 0.46 |
| 5365 | 0.036 | 193 | 15 | 4829 | 0.48 |
| 5171 | 0.035 | 181 | 16 | 5010 | 0.50 |
| 4990 | 0.034 | 170 | 17 | 5179 | 0.52 |
| 4821 | 0.033 | 159 | 18 | 5338 | 0.53 |
| 4662 | 0.032 | 149 | 19 | 5487 | 0.55 |
Failures decrease over time from the beginning. Does this assumption apply to any failure-related event? Yes, we might observe a decreasing failure rate when failures occur due to manufacturing-related issues. In such cases, product fail just after installation. Since they are just a fraction (hopefully!) of the entire population, as soon as they fail, the chance of failure for the rest of population decreases over time.
In this case, a Weibull distribution with shape parameter β < 1can be used for fitting failures.
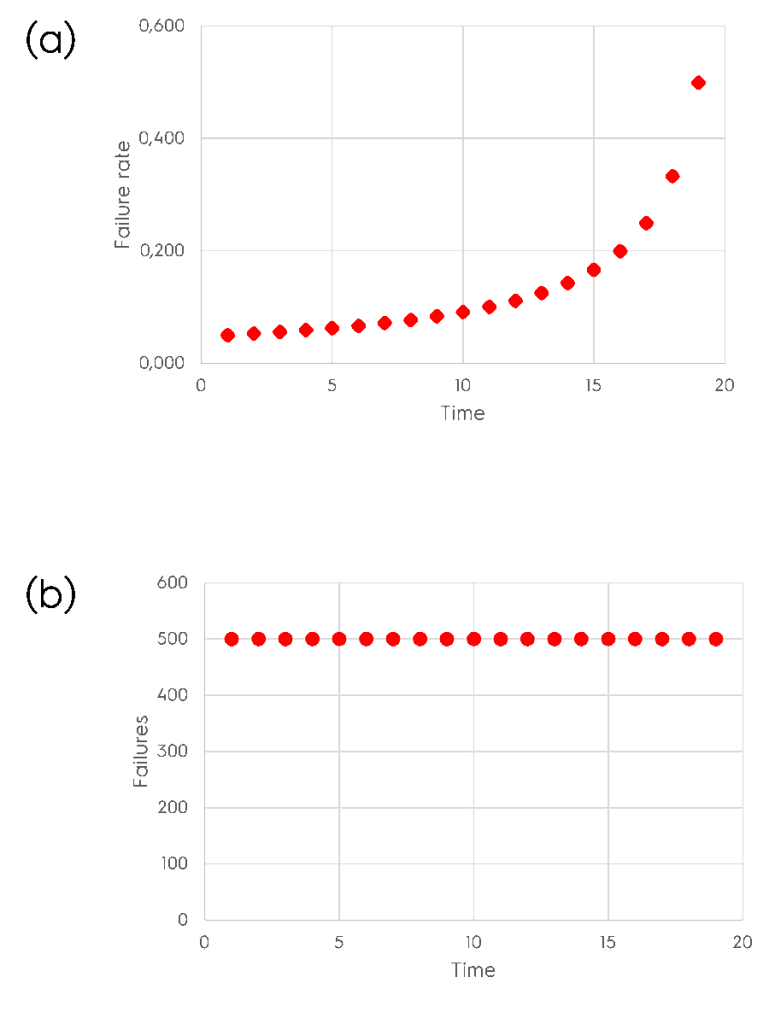
Example 4 – constant number of failures over time.
In this last example, I’ve assumed that the number of failures is constant over time (failures = 500).
Table 4. Example 4: constant number of failures over time. Failures = 500.
| Survival at the beginning of the time interval | Failure rate | Failures | Time interval | Failures (cumulated) | Failure probability |
| 10000 | 0.050 | 500 | 1 | 500 | 0.05 |
| 9500 | 0.053 | 500 | 2 | 1000 | 0.10 |
| 9000 | 0.056 | 500 | 3 | 1500 | 0.15 |
| 8500 | 0.059 | 500 | 4 | 2000 | 0.20 |
| 8000 | 0.063 | 500 | 5 | 2500 | 0.25 |
| 7500 | 0.067 | 500 | 6 | 3000 | 0.30 |
| 7000 | 0.071 | 500 | 7 | 3500 | 0.35 |
| 6500 | 0.077 | 500 | 8 | 4000 | 0.40 |
| 6000 | 0.083 | 500 | 9 | 4500 | 0.45 |
| 5500 | 0.091 | 500 | 10 | 5000 | 0.50 |
| 5000 | 0.100 | 500 | 11 | 5500 | 0.55 |
| 4500 | 0.111 | 500 | 12 | 6000 | 0.60 |
| 4000 | 0.125 | 500 | 13 | 6500 | 0.65 |
| 3500 | 0.143 | 500 | 14 | 7000 | 0.70 |
| 3000 | 0.167 | 500 | 15 | 7500 | 0.75 |
| 2500 | 0.200 | 500 | 16 | 8000 | 0.80 |
| 2000 | 0.250 | 500 | 17 | 8500 | 0.85 |
| 1500 | 0.333 | 500 | 18 | 9000 | 0.90 |
| 1000 | 0.500 | 500 | 19 | 9500 | 0.95 |
Despite the number of survivals decreases over time, the number of failures doesn’t. Do we find something similar in nature? Honestly speaking, we don’t. For this reason, we won’t deal with modeling data shown in Figure 4.
Conclusions
We have seen that different fitting distributions apply to different failure-related phenomena. Exponential, Weibull, and lognormal distributions are the most used functions since they can model failures in different but realistic situations.



 Ask a question or send along a comment.
Please login to view and use the contact form.
Ask a question or send along a comment.
Please login to view and use the contact form.
Thanks Enrico, but I’m a little confused here. Using your definitions for 𝑛(𝑡): number of operational units at time t, and 𝑛0: number of operational units at time t = 0. Then eq2 (that is labelled as the Probability of Failure) should provide the Probability of Failure in Table 1 at row 1 as 0.9; row 2 as 0.81; row 3 as 0.73 etc.
However, if we subtract these from 1 we get 0.1; 0.19; 0.27 etc. This implies that eq 2 is the Probability of Success if column 6 in Table 1 is the Probability of Failure. and as we are using the number of operational units at time t, we are stating the number of operational units that “succeeded”.
In short, eq2 is the Probability of Success, not the Probability of Failure…at least imho.
Dear John,
Eq.2 is the equation of reliability R = n(t)/n0)). It shows the number of samples that are still functioning after a certain time over the number of samples at time 0.
Failure probability is defined as 1-R as you have correctly pointed out.
I will correct the article accordingly.
Thank-you.
Enrico
Some kind suggestions. Figure 1 to 3 have plotted Failure rate and Number of failures, but Figure 4 (a) is a Plot of cumulative number of failure vs. time. This was confusing and impedes learning.
Hi Hammad,
Thank-you for pointing it out. I’ve appreciated it. I’ve corrected the paper accordingly.
cheers,
Enrico