
I have worked in the field of reliability for a good many years. I have presented both beginner and advanced reliability engineering courses. I have even read several books. 🙂 But, across all this, component redundancy has never been explained beyond simple serial and parallel configurations.
So, it was a shock to my system to be presented with a scenario that couldn’t be solved using a simple parallel system.
My previous work had challenged me only as far as:
- Serial
- Active parallel
- Stand-by parallel
- M-out-of-n parallel
- Keystone-component parallel
But now I was being challenged by a network that was none of these.
Network Reliability
Computer networks have been developed that follow more expansive topologies. For example:
- Star
- Bus
- Ring
- Mesh
Many papers have been published on the relative network reliability of these and several variants, but it was even more of a surprise when I could not find a solution to the specific scenario my client was using.
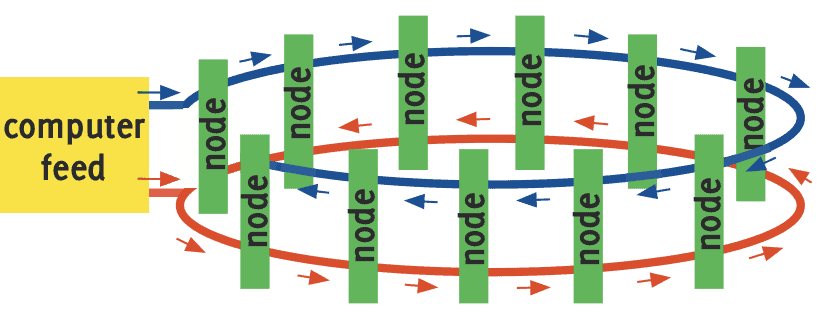
Figure 1: Double-ring topology using separate opposing-direction data feeds.
This topology defines that each node receives 2 independent data-feeds, and the system is considered to be functional if at least one data-feed is received by each node. Multiple breaks in the data-feed are allowed, provided that each node links to the computer feed by either the forward or reverse data-feeds. There is no cross-link between these data-feeds.
I have solved the network reliability for this topology and hope to present at a future reliability conference. However, as a challenge, I invite you to provide a mathematical solution based on:
- Each segment of the data feed, linking adjacent nodes, has a reliability R(t). All segments have equal reliability. There are N nodes, with N forward segments and N reverse segments.
- All nodes must receive data in order for the system to be considered functional. The reliability of each node is not part of the solution – their system contribution is a simple series calculation and would be easily added to the dual-ring topology solution.
- The reliability of the main computer data feed is also not part of the requested solution – as with the nodes, its contribution is a simple series calculation.
And if you identify an already published paper that solves the network reliability for this topology, based on R(t) for each segment, I would of course value a link.
I look forward to hearing from you. Please contact me at Les Warrington
I will also publish a follow-up article on Accendo with my solution in a few weeks.
http://www.pitt.edu/~dtipper/3955/Grover3.pdf looks like it deals with bi-directional ring network availability, assuming independence, constant failure rates, and availability – MTBF/(MTBF+MTTR).
Reliability ~P[both rings survive] + P[one ring fails and other survives] = 2*R(t)^N+ (1-R(t)^N)*R(t)^N This avoids dealing with failure position and reachability.
Hi George,
The article you referenced is interesting. However, the scenario I described does not send data on the 2 rings in the same direction — the data physically travels in opposite directions. Therefore, your deduction that the solution is simply based on either both rings surviving or one ring surviving (the other failing) falls down.
In my scenario, there may be multiple ring segment failures, on both rings, and the system can still provide data to all nodes — the requirement is that ring segment failures must not result in a dead zone with neither forward nor reverse data flow. We do not require all segments in either ring to be operational.
I would also point out that the probability of both rings surviving would be R(t)^2N. Also, your mathematical expression of “one ring fails” indicates that you are considering only the case where ALL segments in that ring fail. This is but one scenario — there are many others.
Thank you again, though, for the article. Informative.
Les
I withdraw my comment “Also, your mathematical expression of “one ring fails” indicates that you are considering only the case where ALL segments in that ring fail”
And, with the correction that the probability of both rings working, your solution reduces to R^n, which is simply serial reliability for one ring. Sorry.
Anyone attending RAMS 2020? If you are, I will be presenting the analytical exact solution for this dual-ring network.
Part of my paper will also illustrate how to combine competing failure modes of single-channel failure (as this topology) and simultaneous dual-channel failure. The real world scenario exhibits both types of failure, thus complicating the situation. However, analytical solution is available — and presented.
If you are not able to attend RAMS 2020, maybe you could access my paper after it is available on the IEEE website. …or contact me directly.