
Extended Bogy Testing
Introduction
Extended bogy testing builds on test to bogy (TTB), discussed in a prior article. TTB focused on calculating the number (N) of parts tested to one life bogy, with 0 failures allowed, to a specified reliability (R) and confidence (C) levels.
Using TTB to verify conformance to high reliability and confidence targets requires very large sample sizes, increasing testing cost. The capacity to test large samples may require large facility capital expenditures. Also, the zero failures allowed paradigm removes the opportunity to learn about product failure modes and the opportunity to improve the product through design or manufacturing process changes.
This article focuses on extended bogy test plans as an alternative to TTB.
Success-Run and Weibull
A success run test plan provides the sample size required when testing to one life bogy with defines reliability and confidence goals, equation 1
$$R^N=1-C$$
(1)
The Weibull reliability equation describes the reliability at any time t, given a characteristic life $-\theta-$ and slope $-\beta-$ for a failure mode, equation 2
$$R(t)=e^{-(t/\theta)^\beta}$$
(2)
By combining the natural logarithm of equations 1 and 2, yields
$$\frac{1}{N}ln(1-C)=-(t/\theta)^\beta$$
(3)
For any desired reliability and confidence, equation 3 allows the calculation of a desired sample size N when tested to time t. To obtain a form that eliminates $-\theta-$, use equation 4
$$\frac{(1/N)ln(1-C)}{(1/N_0)ln(1-C)}=\frac{-(t/\theta)^\beta}{-(t_0/\theta)^\beta}$$
(4)
Which simplifies to
$$N=N_0(t_0/t)^\beta$$
(5)
Equation 5 is combined with equation 1 to yield
$$N=(t_0/t)^\beta(ln(1-C)/ln(R))$$
(6)
Equation 5 relates the test sample sizes (N), for specific reliability (R) and confidence (C) targets, and a test bogy (t0) required for test time t. Variable t may be time, miles, or cycles. The parameter $-\beta-$ is unknown, however, failure modes beyond the life bogy target are usually wear-out failures with $-\beta>1-$. For test planning purposes an accepted approach is to set $-\beta=2-$.
Example 1
Consider a reliability verification test with a target of R99/C90. For TTB, the sample size required is N0=230 parts. If $-\beta=2-$ and t/t0=3, then using equation 4, then the required verification test sample size was reduced to N=26 parts.
Note that this test strategy reduces the test sample size at the expense of increased test time. Also, the test is focusing on wear out failure modes. To minimize the test time penalty, the task of accelerating the test to reduce test time will be discussed in a future article.
Example 2
An automotive electromechanical switch was being tested to verify R95/C90. The TTB sample size was 45 parts, but the supplier’s test fixture could test only 8 parts simultaneously. The extended test bogy was established as 850,000 cycles over 100,000 miles of usage. In this case, $-\beta=1.7-$ was a corporate standard for planning extended bogy testing. Equation 6 was used to determine 2,187,000 cycles were the extended test bogy.
The calculations were incorporated into a visual basic macro. A screen shot of the window is shown in figure 1,
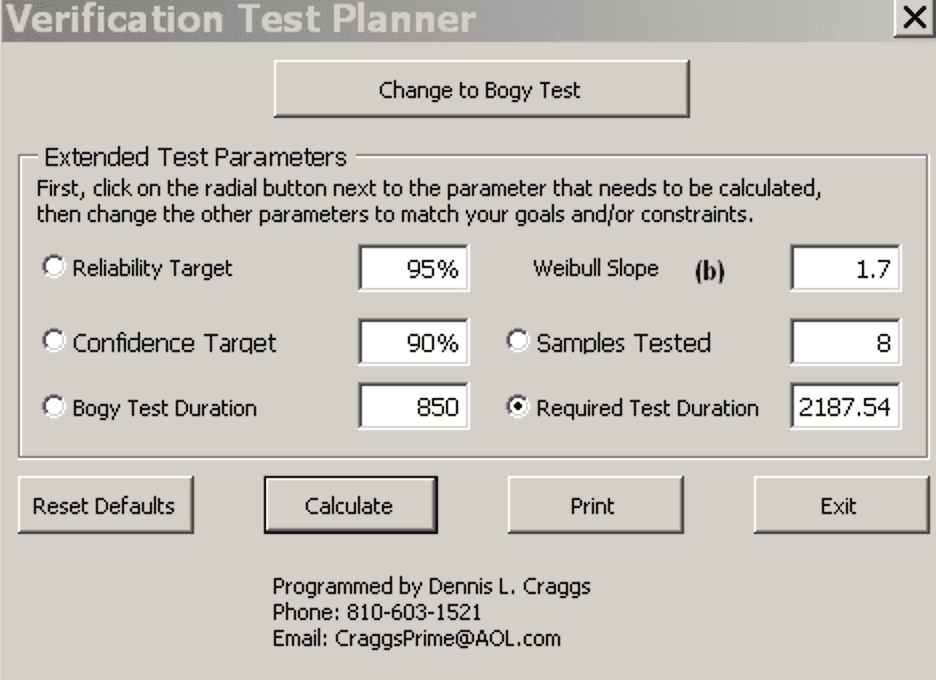
Figure 1
This macro incorporated equations 1 to 5, plus a Bayesian modification to equation 1. It makes it very easy to tradeoff sample sizes with test durations, reliability, confidence, and Weibull slope. However, it is not required as the options can be calculated manually with equation 6.
The test duration was rounded up to 2.2 million cycles. The equipment was able to execute 1 cycle/second and operated 24 hours/day. The test time required was almost 26 days, which was consistent with program timing. During the test, two defects were detected, analyzed, and remove with simple design changes. Later, the improved product was verified to 4,000,000 cycles without failure and there were no reported field failures.
Summary
Extended bogy tests
- Provide a means of reducing the samples required for high reliability and confidence tests.
- Test time is increased, but the capital expenses for additional test facilities are reduced.
- All failures should have the root cause of failure determined.
- Failures prior to one life bogy would be considered a test failure.
- Failures beyond one life would not be considered test failures unless the Weibull analysis showed the R/C targets were not met.
Note
If you want to engage me on this or other topics, please contact me. I offer a free hour for the first contact to discuss your problem/concerns and to determine how I can help you.
I have worked in Quality, Reliability, Applied Statistics, and Data Analytics over 30 years in design engineering and manufacturing. In the university, I taught at the graduate level. I also provide Minitab seminars to corporate clients, write articles, and have presented and written papers at SAE, ISSAT, and ASQ. I want to help solve your design and manufacturing problems.
Dennis Craggs, Consultant
810-964-1529
dlcraggs@me.com
Leave a Reply