
One of the most basic skills needed for the CRE exam is the ability to correctly read the Standard Normal Table.
Writing this short how-to article would be really easy if there were only one way to create the table. There isn’t. It seems every author has to create a unique way to tabulate the values.
Different tables
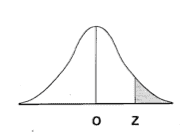
If you noticed, and you should have, there almost always is a small normal curve associated with the table. It will have some portion shaded. Often that shaded area is the value provided in the body of the table for a specific z-value.
As you know, for a given z-value, or distance from the mean in units of standard deviation, the area under the curve or probability is determined.
What changes is which area the author provides.
In the CRE Primer, Appendix X Table III the graphic shows a complete normal curve with the shading of the tail to the right of the z value.
Some tables have the area to the left of the z-value, some have the area from the mean to the z-value. And, the table may be to the left or the right of the mean. There are many possibilities.
The results end up being the same using the symmetry and other properties of the standard normal distribution.
For example, in the case where we’re using the CRE Primer table and calculate a z-value. The table provides the probability represented by the area to the right of the z-value. If instead, we wanted the value to the left, we can use the properties that the area under the curve is equal to one. Thus one minute the value from the table provides our desired result.
Symmetry
Most tables, that I know about, provide probabilities (area under the curve) only for positive z-values. Given the symmetry of the distribution, we just multiply the negative z-value by minus one, use the table to find a value.
I often will draw a normal curve and shade the area of interest to solve the problem. Then compare my drawing to the image on the table and sort out the appropriate actions to take to determine the desired value.
Entering the table
Unlike other distributions, the standard normal distribution does not have different values for specific degrees of freedom. There is only one curve, the standard normal curve.
All that you need to find the area under the curve (probability) is to determine the z-value of interest.
With a z-value, you are ready to enter the table.
Many standard normal tables provide the first two digits along the vertical axis and the third digit along the horizontal axis. Therefore, let’s say we have a z-value of 1.21.
Frist find 1.2 along the left-hand column, then move to the right to the column representing the third digit of interest, in this case, x.x1, to find in the body of the table, 0.1131.
Finding the z-value given an area
The table works in reverse as well. Given an area, find the corresponding z-value.
Let’s say we want to find the z-value corresponding to the right tail (shaded area) corresponding to 10% of the total area under the curve.
Divide by 100 to remove the percentage, thus working with the decimal fraction of the area (a value between zero and one). In this case, we have an area of 0.10.
Scan the internal of the table to find values that encompass the value 0.10. In the CRE Primer table, that would be 0.1003 and 0.0985. The position of 0.1003 corresponds to (along the left column) the first two digits of 1.2 and (in the column) to the third digit of x.x8. Resulting in a z-value of 1.28.
There is that 0.003, so the z-value is just a little to the right, 1.28 plus a little. We could use interpolation to find the z-value to the desired precision. In this case, 1.28 is good enough for me.
Summary
In short, the tables are easy to read. z-value along outside edges, areas under the curve (probabilities) in the body of the table.
Draw a curve and shade the area and mark the z-value represented in the problem you’re trying to solve.
Compare the desired values to the drawing associated with the table and adjust as needed to convert the table value to the solution.
Remember the basic properties of a standard normal, especially the symmetry and the total area is equal to one.
With a little practice, you will do fine. I do recommend practicing using the same table you plan on using in the exam – as during the exam a simple mistake is still a missed problem. Make it easy on yourself and use the same table in the exam as in practice.
Related:
Reading a Standard Normal Table (article)
z value (article)
Interpolation within Distribution Tables (article)
Leave a Reply