Measuring and Improving Your Chance of Business Process Success 

 An endless Dilemma confronts every business. It is how to ensure that the activities we undertake will always produce the intended results. 

Explosions, workplace deaths, harmful accidents, physical injuries, damaged goods, scrapped jobs, repeat work, manufacturing errors, operating mistakes, bad repairs, misunderstanding, wrong decisions, supplier miscommunication and poor delivery performance are all examples of the many unwanted troubles and problems caused by the Dilemma. Its impacts and effects have been written about for more than 6,000 years of recorded human history. 

The Dilemma’s prevalence throughout the world indicates that human beings are a major contributor. A second major factor is business design: how your processes are configured and operate determines your degree of success in addressing the Dilemma. A third big cause is our training and education processes which have transferred the Dilemma all through businesses and across cultures for over 60 centuries. To stop the Dilemma affecting your company you can use what we have learnt about the universe, people and business processes during the last 100 years. 

Keywords: distribution plot, business process measurement, process capability, business process improvement 

 Processes are everywhere. All our thought processes are sequential. All work is a sequence of tasks. We make meals in our kitchens by following recipes. Business processes are ordered chains of work done one after the other. Everywhere processes are used to achieve an intended outcome. We complete a process and at the conclusion we have reached its goal. At least that is what we hoped to do. 

We can only hope to reach the intended result because we are not in total control of what happens as we move through a process—randomness and chance are always present everywhere. 

Chance is built into the way the Universe works. As the scale of matter increases—subatomic to atomic, atomic to molecular, molecular to cellular in living tissue and granular in lifeless solids, cellular and granular to structure, structure to complex organisation, complex organisation to massive complexity, massive complexity to worlds and planets, worlds to far flung galaxies—it is impossible to know exactly what will happen after each transition point. The behaviour and outcomes within each zone of separation cannot be determined from the prior¹. The spans between subatomic particles to rushing galaxies are bridged by paths of randomness. It makes absolute prediction impossible. Which atom becomes a star or becomes you is unknowable. This uncertainty is how the Universe works; maybe one distant day will understand why it is so. 

Chance always permits a range of outcomes. We cannot know with total certainty what will happen as our human and worldly processes go from simple inputs to greater complexity. Because of the presence of Chance, we configure businesses to work in ways that increase certainty. We set desired business policies. We impose processes and rules on people through procedure. We 

train and educate ourselves and our children to conform to set standards. But none of that stops errors, failures and disasters happening regularly. 

If we are to positively change our business future (perhaps even our global future) we must learn to manage Chance and understand its Uncertainty. We cannot eliminate Uncertainty in this universe, but through good process design we can manage its variables to produce a range of satisfactory outcomes. I hope that by the end of this paper you learn how to ‘see’ Chance and how to start successfully managing uncertainty in your business processes. 

Measuring Chance, Opportunity, Consequence, Risk 

The great scientist Albert Einstein warned us, “Make things simple, but no simpler.” We did not heed that warning when it came to the risk equation. The risk equation has been simplified too far to the common form below. 

Risk ($/yr) = Consequence of Occurrence ($) x Frequency of Occurrence (/yr) 

It is so cut down in its explanation of risk that it has lost much usefulness in understanding how to fully manage risk events. 

The full risk equation divides Frequency of Occurrence into its two missing components of Opportunity and Chance to become: 

Risk ($/yr) = Consequence ($) x [No. of Opportunities to Fail (/yr) x Chance of a Failure at Each Opportunity] 

In its full form the risk equation gives us three options to control risk—remove the consequences, prevent opportunities arising, and should opportunity arise then limit the probability of the event’s occurrence. If you do not want to die from a shark attack the risk equation gives you options to: 

• • swim with sharks that do not bite (no bad consequence from the action) 
• • swim in water where a shark cannot go (no opportunity for a shark to be present) 
• • swim in water where sharks do not want to go (an insignificant chance to get bitten) 

The risk equation is normally used to measure adverse risk where consequences are expected to be bad. Risk can also be good. Winning a lottery is usually seen as good risk. Good risk has the same equation as bad risk with the focus changed from negative consequences to positive ones. 

The risk equation can be reconfigured to show the Chance of Success instead of the Chance of Failure. In mathematics the Chance of Success is not the opposite of the Chance of Failure. The Chance of Success is what is left over once the Chance of Failure is removed. How success and failure interact mathematically is shown in the following equation. 

Chance of Success = 1 – Chance of a Failure 

Success is certain if failure cannot happen. We can now do some equation manipulation to replace chance of failure with the chance of success. 

Risk ($/yr) = Consequence ($) x [No. of Opportunities (/yr) x {1 – Chance of Success at Each Opportunity}] 

Since the term ‘1 – Chance of Success’ is also known as ‘Uncertainty’, the equation can also be written as: 

Risk ($/yr) = Consequence ($) x [No. of Opportunities (/yr) x Uncertainty at Each Opportunity] 

This change makes the risk equation universal—it now applies everywhere for everything. When consequence is zero risk is zero. When opportunity is zero risk is zero. When uncertainty is zero so too is risk. With this form of the risk equation, we can ‘see’ and measure risk for all things. 

If you want to increase your good risk of winning a lottery then buy lots of tickets so you have many opportunities to win. If you want to be sure to win then buy all the tickets so every opportunity is yours. But if you want to buy just one ticket and still be sure to win you must then remove the uncertainty by guaranteeing the result. That means you must rig the draw. Now your risk turns bad because you will eventually go to gaol (‘jail’ in USA) as well. With the risk equation you have a way of measuring how likely and costly are the range of possible outcomes in a situation. 

Measuring Business Process Success 

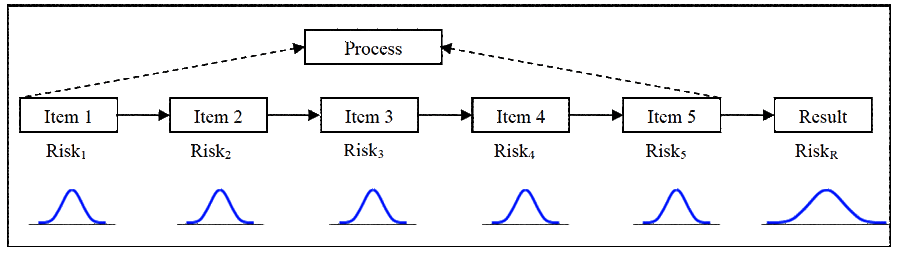
Everything we do is a series of steps accumulated together to form processes. Work is a series of activities. A cool drink maker uses a production process with machines in series to make their product. A Lawyer follows designated protocol when developing and making their case. An education system follows a curriculum that takes students through a subject topic after topic. Making a cake follows the series of tasks in the recipe. If you can show a thing as a flow diagram with an output, like that of Figure 1, then you have got a process. They are everywhere. 

The risk at any time in every step depends on three factors—the consequence of a event, the number of opportunities for the event to happen, and the chance that the event will happen when the opportunity is present (this is its ‘uncertainty’). Each process step has possibilities for many errors and so every process step always has many chances to failure. In Figure 1 the total individual step risk is indicted by the word ‘Risks’ and its subscript. 

Risk exists for every process because Chance exists in every process step. A process goes wrong once any step in it is done wrong. You determine the risk in each step of a process and the combination of all step risks is the risk for the whole process. The mathematics for combining risks is well understood but it can be difficult to do. Usually, risk is mathematically modelled on a computer where the effect of changing the values for opportunity and uncertainty are easily done and the result quickly presented. 

For each process step a distribution of possibilities exist for its result (‘distribution’ is maths-speak—it is the range of possible outcomes). Because variation exists in all things all the time the number of opportunities for an event to arise during a specific period can range from zero to many. 

C:\Users\Mike\Documents\LRS\www\plant-wellness-way.com\PDF Pages Updated to PWW\Measuring and Improving the Chance of Business Process Success.docx 

The chance that situations will go bad can be zero through to totally certain. Risk fluctuates and our task in business is to control opportunity and chance to what is acceptable. 

The curve in Figure 2 is a distribution for a variable being observed. The variable is on the horizontal axis and its values go from low to high. How often a value occurs also varies and the frequency of occurrence is shown on the vertical axis. The distribution curve is the signature of a process. The late quality guru W. Edwards Deming said the curve is the process ‘talking to us’². With a distribution curve you can see the influence and effect of Chance on your business. 

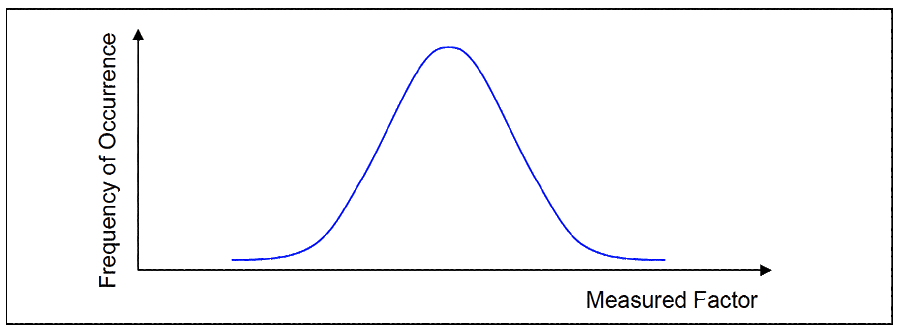
Figure 3 is the production distribution curve for a crushing and processing plant over a two-month period. Once you know that the design rate is 1500 tonne per hour, and it can sell all that it can make, you immediately see that there are huge opportunities being lost by this business. 

In Figure 4 the distribution curves under each step indicate that a range of outcomes are possible for each one of them. Their combination becomes the risk for the process result.

Plot Your KPI Distributions 

The quickest and simplest way to see your outcome distributions and process step distributions is to graph them. Every business record selected Key Performance Indicators (KPI) from throughout their operation. The KPI data is collected at preselected time intervals to later be displayed in reports. Figure 5 indicates where the KPI values reside in the distribution plot. The frequency is the count of the times that a KPI value appeared during the period investigated. The curve of a KPI is not always a normal distribution, but we will use the normal probability curve throughout this article to keep the explanation simple.

Your distributions perfectly reflect how your business works! Because the data comes from your business, the distribution is an exact representation of the outcomes your business produces. Your distribution plots show you the outputs caused by your current business process design—a distribution curve is what your business does to itself! If you change the process design, you will change the distribution of its results. The challenge is to change the process in the right way to always produce only the outcomes that you want. 

To get management worth from your distributions you need to superimpose the KPI limits that management have set. In Figure 6 the required KPIs are overlayed on the distribution. You can see that management have set performance requirements that the process can usually deliver, but which occasionally it cannot. If Figure 6 were a real plot, then the outliers, the distant areas at either side of the curve, would be unacceptable results.

In Figure 7 the required performance is superimposed on the crushing and processing production plant of Figure 3. Now it is clear to everyone that this operation is well short of acceptable.

Understanding Why Business Processes Vary 

A distribution plot of performance results identifies the chance that a result will occur. In Figure 7 the plant runs to management specification about 20% of the time. The distribution of your business and production KPIs are the natural outcomes of the processes you use. If you are concerned with the poor results of your outliers, it becomes necessary to investigate why they happened and then remove their cause(s) through proper process redesign. 

Investigation of business process performance starts with the flow diagram of the process under analysis. Just for the fun of it we will examine a cake making process. But the same approach would be applied if you were building rocket ships to go to planet Mars. Going to Mars is but a combination of processes that produce a desired outcome. 

Our cake recipe is that of Figure 8 (in business and industry you call the ‘recipe’ to make your product or deliver your service a standard operating procedure or a work instruction).

The recipe is first turned into the process flow diagram of Figure 9. The more than twenty tasks in the recipe combine into chains of activities—the cake production process. Each task has one best way to be done, but it has many, many ways of being done wrong. The flow diagram makes clear that great risks exist with every cake you make. Chance awaits you with both success and disaster as its gift if you use this recipe; with disaster being far more likely than success! 

Once a flow diagram is available you can deeply analyse where problems are going to come from in a process. Though every task has a range of outcomes that will affect the final product, not every task is equally important in making a great cake. If you want to make a perfect cake you must do the important tasks, those in the red boxes of the recipe, close to perfect every time. The other tasks can be done ‘good enough’ but the important tasks must be ‘in tolerance’. Most problems would be impossible to spot if you only used the written recipe. You need the flow diagram to get a full understanding of your process risks; words alone are useless! 

Using the recipe alone is not enough to guarantee an eatable cake. The advice given for making the cake right-first-time is pathetically inadequate. There are few indications of task quality 

requirements. There is no sign of which steps are vital to get right, nor of what right is for each step. Because no quality standards have been set all is guesswork. Anyone who is not a chef trying this recipe for the first time would fail to make a good cake unless it was their lucky day. 

The recipe does not provide certainty. Nowhere are you asked to prove the quality of anything. Every step depends on you already knowing what the chef who wrote the recipe knew. Until you learn from your mistakes you will make many poor cakes because the distribution curves for the variables in the recipe are huge. As an example, in Figure 10 the variable for the ‘bake in oven’ step is plotted as a distribution with the intended performance KPI range overlayed. With this curve you cannot expect to bake many cakes that you can eat—about half of the baked cakes will be unacceptable. What you really want is the ‘correctly baked’ cake distribution shown in Figure 11—where every cake is properly baked no matter who bakes it. 

Figure 10 is only for the one recipe step ‘bake in oven’, but variations will arise with every step. You really need to see the distribution curves for all the problem variables to get a true understanding of how likely it is that you will get an eatable product when this process is used. 

If your company procedures and work instructions are written without task quality controls, like with the cake recipe, then you naturally get a wide performance distribution curve. In such 

distributions much of the result depends on Chance. Your people, supervisors and managers will learn from their mistakes, but they will make many mistakes at great cost to your company as they learn. And if those knowledgeable persons, then leave your company, you will again end up training their replacements by the hugely expensive failure-and-trial method you have created. 

Changing Processes so Outcomes are More Likely to Be Successful 

Both poor and great results will happen when a distribution is wide. This creates endless frustration for managers because from the same process the outcomes can be wonderful one day and a disaster the next. To always get the ideal cake, the result of every task in the recipe must always be within its desired performance limits. To achieve that with certainty you have to build a process where every step in the cake recipe is done right every time. The full risk equation below tells us that to create certainty in each step you must remove all uncertainty. 

Riskn = Consequencen x [ No. of Opportunitiesn x Uncertainty at Each Opportunityn ] 

The obvious thing to do for a start is to rewrite and flow chart the recipe so that it is helpful to the cook. Added into the flow diagram of Figure 12 are step quality requirements—what is and is not acceptable at each step. Tell the cook the quality KPI range for each task—what are the pass-fail criteria for acceptance. Where you must make decisions based on visual information provide photographs of pass and fail criteria. Where you can measure to get accurate control include measurements to confirm acceptable performance. Introduce proof tests to verify the step result is in the allowable quality range. If the work is so complex as to confuse people, then show a video of how to do a task right. You will even go as far as to have an audio description spoken aloud as people do the tasks if that will ensure the task variability is significantly reduced. 

Setting Quality Standards and Keeping Quality Standards 

When a business process is designed it is the responsibility of the Business’ Management to set the quality standards for all the variables that affect task performance and process results³. Once the process is in operation the performance quality standards are up-held by the company’s supervision—they are the process ‘policemen’. 

Improving the Process is Everyone’s Role 

The best way to manage risk in your processes is to set your people required step KPIs and show them a graph of their performance distribution. Secondly, invite everyone working in a process to continually look for new and creative ways to ‘make it better’. No process design is ever perfect, and every process can always be improved. A manager’s role is to move their processes up the best practise quality path of ‘good-better-best’ as rapidly as possible. 

My best regards to, 

Mike Sondalini 

—

1  Laughlin, Robert B., A Different Universe (reinventing physics from the bottom down), Basic Books, 2005

2 Deming, W E., Out of the Crisis, MIT Press, London, England, 2000 edition

3 Deming, W E., Out of the Crisis, , MIT Press, London, England, 2000 edition