
Published in Quality Progress in Nov. 2018, pp 34-39. Final 1/27/18 Posted here with permission of Dr. Wayne Nelson and by his suggestion.
PREDICTING REPAIR RATES WITH PLOTS
Guest post by: Wayne B. Nelson, consultant
Schenectady, NY , WNconsult@aol.com
1. INTRODUCTION
Purpose. This article presents a simple and informative plot for analyzing test and field data on repeated repairs of a sample of systems. Reliability textbooks lack this useful new plot which here is used to:
- Predict future population numbers of repairs, for example, during system warranty or design life,
- Evaluate whether the population repair rate increases or decreases with age (this is useful for making decisions on factory burn-in, preventative replacement in service, and system retirement).
- Nelson (2003) gives other repair and recurrent-event applications and information on
- Comparing two or more data sets, which may come from different designs, vendors, production periods, environments, maintenance policies, etc.
- Analyzing repair cost data or other numerical values associated with repairs (e.g., downtimes),
- Analyzing data with a mix of types of repairs,
- How plots reveal unexpected and useful information,
- Analyzing availability data, including downtime for repairs,
- Analyzing data with more complex censoring where system histories have gaps with missing repair data,
- The minimal assumptions underlying the non-parametric estimate and confidence limits here.
Cook and Lawless (2007) present such analyses of data on recurrent diseases, software errors, and other types of recurrences.
Overview. Section 2 describes typical repair data. Section 3 presents the basic population model and its informative mean cumulative function (MCF) for the number of repairs. The MCF provides desired information. Section 4 presents the plot of the MCF estimate and explains how to use and interpret such plots. Section 5 shows how to calculate and plot an estimate of the MCF.
2. REPAIR DATA
Transmission. This section describes typical repair data from a sample of systems. Table 1 presents typical repair data on a sample of 34 preproduction cars in a severe track test. Information sought from the data includes (1) the mean cumulative number of repairs per car by 24,000 test miles (equivalent to 132,000 customer miles, design life) and (2) whether the population repair rate increases or decreases as the population ages. For each car, the data consist of the car’s mileage at each transmission repair and its latest observed mileage. For example, the data on car 024 are a repair at 7068 miles and its latest mileage 26,744+ miles; here “+” indicates this is how long the car has been observed. Nelson (2003) gives other repair data on blood analyzers, residential heat pumps, window air-conditioners, power supplies, turbines, and other applications. The plot applies to recurrence data from many fields, for example, episodes of recurrent diseases, falls of the elderly, and customer purchases on Amazon.com.
| Table 1 Automatic Transmission Repairs | |||
| CAR | M I L E A G E . | ||
| 024 | 7068 | 26744+ | |
| 026 | 28 | 13809+ | |
| 027 | 48 | 1440 | 29834+ |
| 029 | 530 | 25660+ | |
| 031 | 21762+ | ||
| 032 | 14235+ | ||
| 034 | 1388 | 21133+ | |
| 035 | 21401+ | ||
| 098 | 21876+ | ||
| 107 | 5094 | 18228+ | |
| 108 | 21691+ | ||
| 109 | 20890+ | ||
| 110 | 22486+ | ||
| 111 | 19321+ | ||
| 112 | 21585+ | ||
| 113 | 18676+ | ||
| 114 | 23520+ | ||
| 115 | 17955+ | ||
| 116 | 19507+ | ||
| 117 | 24177+ | ||
| 118 | 22854+ | ||
| 119 | 17844+ | ||
| 120 | 22637+ | ||
| 121 | 375 | 19607+ | |
| 122 | 19403+ | ||
| 123 | 20997+ | ||
| 124 | 19175+ | ||
| 125 | 20425+ | ||
| 126 | 22149+ | ||
| 129 | 21144+ | ||
| 130 | 21237+ | ||
| 131 | 14281+ | ||
| 132 | 8250 | 21974+ | |
| 133 | 19250 | 21888+ | |
Censoring. A system’s latest observed age is called its “censoring age”, because the system’s repair history beyond that age is censored (unknown) at the time of the data analysis. Usually, system censoring ages differ. The different censoring ages complicate the data analysis and require the analysis in Section 5. If a system has no failures; then its data are just its censoring age, e.g., car 031. Other systems may have one, two, three, or more repairs before its censoring age.
Age. Here “age” (or “time”) means any useful measure of system usage, e.g., mileage, days, cycles, months, etc.
3. THE POPULATION MODEL AND ITS MEAN CUMULATIVE FUNCTION
Model. The following is a nonparametric model for the population. At age t, population system i has accumulated a total cost Ci(t) (or number) of repairs. To simplify, Figure 1 depicts just six population Ci(t) as smooth curves for ease of viewing. In reality each Ci(t) is a staircase function where the rise of each step is system i’s cost (or number) of repairs at that age. Ci(t) is called a system’s cumulative history function for cost (or number) of repairs. The nonparametric population model is the collection of all population Ci(t). In this model, all Ci(t) extend uncensored to any age of interest. Censoring is a property of the sample data, not of the model. It is assumed that one has a statistically random sample of systems.
MCF. At any age t, there is a population distribution of the cumulative cost (or number) of repairs, which appears in Figure 1 as a continuous density for cost. For the cumulative number of repairs, this distribution is discrete with integer values 0, 1, 2, etc. The distribution at age t has a population mean M(t). In Figure 1, M(t) as a function of t is the dark line. M(t) is called the population “mean cumulative function” (MCF) for the cost (or number) of repairs. It provides most of the information sought from repair data. The population M(t) is a staircase function with many small steps. In practice, M(t) is usually regarded as a smooth curve. M(t) is the vertical population average of all the population Ci(t). M(t) is analogous to the cdf F(t) of a life distribution but has a different meaning and interpretation. M(t) can exceed 1, since the mean number of repairs per system can exceed 1.
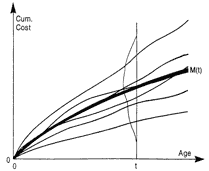
Repair rate. When M(t) is for the number of repairs, the derivative
m(t) = dM(t)/dt
is assumed to exist and is called the population “(instantaneous) repair rate”. It is also called the “recurrence rate”. It is expressed in repairs per unit “time” (the measure of usage) per system, e.g., transmission repairs per 1000 miles per car. Some mistakenly call m(t) the “failure rate”, which causes confusion with the quite different failure rate (hazard function) of a life distribution for non-repaired units (e.g., failed components that are discarded). The failure rate for a life distribution has an entirely different definition, meaning, and use; this is explained by Ascher and Feingold (1984).
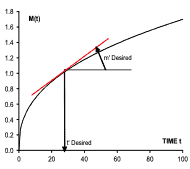
Burn-in. Repair rate is used to determine the length of a factory burn-in. Then systems are run and repaired until the population repair rate decreases to a desired value m’. Consequently systems in service do not experience the high initial repair rate. An estimate of the needed length t’ of burn-in is obtained from the MCF as shown in Figure 3. A straight line segment with slope m’ is moved until it is tangent to the MCF. The corresponding age t’ below the tangent point is the desired burn-in time.
4. HOW TO INTERPRET AND USE A PLOT
MCF estimate. Figure 2 is a plot of the unbiased estimate M*(t) of M(t) for the transmissions. Software described below calculate and plot this nonparametric estimate, which involves no assumptions about the mathematical form of M(t) or the process generating the system histories. M*(t) is a staircase function that is flat between repair ages, but the flat portions need not be plotted. The MCF of a large population is usually regarded as a smooth curve; thus one usually imagines a smooth curve through the plotted points. Interpretations of such plots appear below. See Nelson (2003) for more detail.
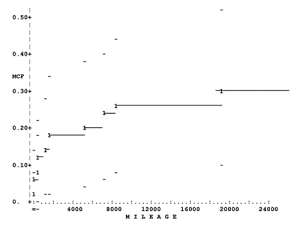
Mean cumulative number. An estimate of the population mean cumulative number of repairs by a specified age is read directly from such a curve through the plotted points. For example, from Figure 2 (or Table 2 below), the estimate M*(24,000 miles) is 0.31 transmission repairs per car, information that was sought. This high valued indicated that improvements were needed. The plot shows Nelson’s (1985) approximate confidence limits for M(t) as a “–” above and below the M*(t) staircase at each repair age. In theory each “−” extends to the next repair age, but these line segments are omitted here for simplicity. The two-sided 95% confidence limits for M(24,000) in Figure 2 are 0.10 and 0.52 transmission repairs per car.
Repair rate. The derivative of such a curve (imagined or fitted) estimates the repair rate m(t). If the derivative increases with age, the population repair rate increases as systems age. If the derivative decreases, the population repair rate decreases with age. The behavior of the rate is used to determine burn-in, overhaul, and retirement policies. Figure 2 shows that the transmission repair rate decreases with mileage. Consequently preventive replacement does not reduce transmission failures in service. Preventive replacement is used for jet engine components.
Software. The following commercial software calculate and plot the MCF estimate and Nelson’s (1995) confidence limits for M(t) from data with exact ages and right censoring. The complex calculation of these limits requires such software. These software analyze both the number and cost (or value) of recurrences and handle positive and negative values.
Minitab 18 “Overview of Nonparametric Growth Curve,” https://support.minitab.com/en-us/minitab/18/help-and-how-to/modeling-statistics/reliability/how-to/nonparametric-growth-curve/before-you-start/overview/
JMP 13 of SAS Institute, JMP 13 Reliability and Survival Methods, Section 6 Recurrence Analysis, https://www.jmp.com/content/dam/jmp/documents/en/support/jmp131/Reliability-and-Survival-Methods.pdf
The RELIABILITY Procedure in the SAS/QC Software SAS/QC 9.3 User’s Guide, “Recurrence Data from Repairable Systems,” https://support.sas.com/documentation/cdl/en/qcug/68161/HTML/default/viewer.htm#qcug_reliability_details58.htm
Recurrence Data Analysis (RDA) of ReliaSoft’s Weibull++ software, http://reliawiki.org/index.php/Recurrent_Event_Data_Analysis
Literature. Most previous models and data analysis methods for repair data apply only to counts of repairs – not costs. They are parametric and involve more assumptions, which often are unrealistic. For example, Englehardt (1995) and Ascher and Feingold (1984) present such models, assumptions, and analyses for counts of repairs of a single system, not for a sample of systems. The simplest parametric model for counts of repairs is the Poisson process. Nelson (2003) and Cook and Lawless (2007) extend methodology to costs, downtimes, and other values associated with repairs, whereas previous methods apply only to simple counts of repairs.
Concluding remarks. The simple plot of the sample MCF is informative and widely useful. It requires minimal assumptions and is simple to make and present to others.
5. CALCULATION OF THE MCF ESTIMATE AND ITS PLOT
Calculation. This section shows the simple calculation of the MCF estimate for those who wish to use a spreadsheet like Excel to make their own plots; this will require the use of a variable that is 1 for each repair and 0 for each censoring age. The following steps yield an unbiased nonparametric estimate M*(t) of the population M(t) for the number of repairs from a sample of n systems; for the transmissions, n = 34 cars.
1. List all repair and censoring ages in order from smallest to largest as in column (1) of Table 2. Denote each censoring age with a +. If a repair age of a system equals its censoring age, put the repair age first. If two or more systems have a common age, list them in a suitable order, possibly random.
2. For each sample age, write the number r of systems that ran through that age (“at risk”) in column (2) as follows. If the earliest age is a censoring age, write r = n1; if a repair age, write r = n. Proceed down column (2) writing the same r-value for each successive repair age. At each censoring age, reduce the r-value by one. For the last censoring age, r = 0.
3. For each repair, calculate its observed mean number of repairs per system at that age as 1/r. For example, for the repair at 28 miles, 1/34 = 0.03, which appears in column (3). Only two decimal places are shown here for easy reading. For a censoring age, the observed mean number of repairs is zero, corresponding to a blank in column (3). However, the censoring ages determine the r-values of the repairs, thereby censoring ages are properly taken into account.
4. In column (4), calculate the MCF estimate M*(t) for each repair age as follows. For the earliest repair age, this is the corresponding mean number of repairs per system, namely, 0.03 in Table 2. For each successive repair age this is the corresponding mean number of repairs (column (3)) plus the preceding mean cumulative number (column (4)). For example, at 19,250 miles, this is 0.04+0.27 = 0.31. Censoring ages have no mean cumulative number.
5. For each repair, plot on graph paper its mean cumulative number (column (4)) against its age (column (1)) as in Figure 2. This plot displays the non-parametric estimate M*(t), which is a staircase function. Censoring times are not plotted but are taken into account in the MCF estimate.
| Table 2. MCF Calculations | |||
| (1) Mileage | (2) No. r obs’d | (3) mean no. 1/r | (4) MCF |
| 28 | 34 | 0.03 | 0.03 |
| 48 | 34 | 0.03 | 0.06 |
| 375 | 34 | 0.03 | 0.09 |
| 530 | 34 | 0.03 | 0.12 |
| 1388 | 34 | 0.03 | 0.15 |
| 1440 | 34 | 0.03 | 0.18 |
| 5094 | 34 | 0.03 | 0.21 |
| 7068 | 34 | 0.03 | 0.24 |
| 8250 | 34 | 0.03 | 0.27 |
| 13809+ | 33 | ||
| 14235+ | 32 | ||
| 14281+ | 31 | ||
| 17844+ | 30 | ||
| 17955+ | 29 | ||
| 18228+ | 28 | ||
| 18676+ | 27 | ||
| 19175+ | 26 | ||
| 19250 | 26 | 0.04 | 0.31 |
| 19321+ | 25 | ||
| 19403+ | 24 | ||
| 19507+ | 23 | ||
| 19607+ | 22 | ||
| 20425+ | 21 | ||
| 20890+ | 20 | ||
| 20997+ | 19 | ||
| 21133+ | 18 | ||
| 21144+ | 17 | ||
| 21237+ | 16 | ||
| 21401+ | 15 | ||
| 21585+ | 14 | ||
| 21691+ | 13 | ||
| 21762+ | 12 | ||
| 21876+ | 11 | ||
| 21888+ | 10 | ||
| 21974+ | 9 | ||
| 22149+ | 8 | ||
| 22486+ | 7 | ||
| 22637+ | 6 | ||
| 22854+ | 5 | ||
| 23520+ | 4 | ||
| 24177+ | 3 | ||
| 25660+ | 2 | ||
| 26744+ | 1 | ||
| 29834+ | 0 | ||
Cost. The MCF estimate for cost (or value) data is obtained with the same calculation where the mean number 1/r for a repair is replaced by C/r where C is the cost of that repair.
Acknowledgments. The author gratefully acknowledges his client Mr. Richard J. Rudy of Daimler-Chrysler, who generously granted permission to use the transmission repair data here. The author thanks the referees for contributions to a clearer version of this article.
REFERENCES
Ascher, H. and Feingold, H. (1984), Repairable Systems Reliability, Marcel Dekker, New York.
Cook, R.J. and Lawless, J.F. (2007), The Statistical Analysis of Recurrent Events, 420 pp., Springer, New York.
Englehardt, M. (1995), “Models and Analyses for the Reliability of a Single Repairable System,” in N. Balakrishnan (ed.), Recent Advances in Life-Testing and Reliability, 79- 106, CRC Press, Boca Raton, FL.
Nelson, Wayne (1995), “Confidence Limits for Recurrence Data – Applied to Cost or Number of Repairs,” Technometrics 37, 147-157.
Nelson, Wayne B. (2003), Recurrent Events Data Analysis for Product Repairs, Disease Recurrences, and Other Applications, 151 pp., ASA-SIAM, Philadelphia, www.siam.org/books/sa10 .
 Ask a question or send along a comment.
Please login to view and use the contact form.
Ask a question or send along a comment.
Please login to view and use the contact form.
What if you need the probability distribution of N(t) or N(t)-N(t-1) and you don’t have lifetime data? Imagine working in automotive aftermarket and want to recommend stock levels of spare parts to satisfy fill rate or service level goals. The only data you have is vehicle installed base in store neighborhoods, catalogs that tell which parts go into which cars, and monthly sales by part number.
MCF = E[N(t)] and its confidence limits are limits on the mean, not tolerance or prediction limits on random variables N(t) or N(t)-N(t-1), needed for stock level recommendations.
Hi Larry,
Have you tried Poisson distributions for your spare part quantification? With that you can define your risk of stock-out (=1-service level), consider an average lead time and get your desired count of spares.
Thanks. I learned actuarial methods working for the US Air Force Logistics Command on engines. They make actuarial forecasts and assume demand distribution is Poisson. Actuarial forecast is the demand mean, and, conveniently, the mean of a Poisson distribution is also the variance.
However, I extended actuarial methods to all service parts, without life data, using installed base, gozintos, and parts’ consumption counts. When I worked in the automotive aftermarket, we assumed parts’ demands had Poisson distribution. If your auto parts store did not have the part you wanted in the late 1990s, it could have been my fault. http://www.Epicor.com has reverted to forecast = N/MTBF. Sorry. I keep trying to do better, while others try to do simple.
The martingale central limit theorem says the asymptotic parts’ demand distribution is Normal with mean demand equal to actuarial forecast and DIFFERENT variance from the actuarial forecast. I am working on the variance-covariance computations now. Stay tuned to Fred’s weekly reports.
If you would like me to adapt the martingale central limit theorem for a renewal process demand distribution and actuarial forecast, send some data and describe it.
Thanks for your interest.
Informative article. Excellent! I could reproduce M(t) and Figure 2 using ReliaSoft.
Two questions by the way:
1) I wonder how to interpret M(t), knowing that it can get values less or more than 1. For instance in the case of the given example, if I have M(t)=0.314, does it say anything to me without looking into the staircase graph?
2) Doesn’t it matter if those failure modes causing the failure events be similar or different?
Cheers,
Keyvan