Process Capability Analysis I – Overview and Indices

Introduction

How is a manufacturing process determined to be capable of producing parts that meet engineering requirements? Some, like the finish of a gear tooth are critical, while the roughness of a non-contact surface isn’t critical. The critical characteristics need to be identified and checked to determine if the process is capable.

This article defines the analysis concepts and indices.

Prototypes and Series Production

Process capability assessments (PCA) start during the product development process and continue into series production. Prototype parts are created by a variety of methods, ranging from hand-crafted parts to short term manufacturing in a production intent process under factory conditions. The methods that are closest to series production are the most realistic.

The Data

The data collected on critical characteristics show a central value and variation. It is relatively easy during development and during serial production to adjust the central value while variation is hard to control. A normal distribution provides a good model for many measurements.

For prototype part data the sample mean, $-\bar{X}-$, and standard deviation, s, are calculated, using equations 1 and 2.

$$\bar{X}=\sum_{i=1}^{i=N}X_i$$

(1)

$$s^2=\sum_{i=1}^{i=N}\frac{(X_i-\bar{X})^2}{N-1}$$

(2)

For serial production, SPC can be used to estimate the process mean and standard deviation. If  $-\bar{X}-$ and R charts are used, then the overall process average, $-\bar{\bar{X}}-$, and the standard deviation, s, are calculated using equations 3 and 4.

$$\bar{\bar{X}}=\sum_{j=1}^{j=N}{\bar{X}_j}$$

(3)

$$s=\frac{\bar{R}}{d_2}$$

(4)

The average and standard deviation are used to estimate the normal distribution parameters, $-\mu-$ and $-\sigma-$, ignoring sample variation. The 3$-\sigma-$ limits of the distribution are calculated using equation 5.

$$\mu\pm3\sigma$$

(5)

Note the distribution 3$-\sigma-$ limits have a range of 6$-\sigma-$.

A Centered Process

When there is a two-sided engineering specification, the middle of the tolerance range is the usually the process target. In some specifications, there may be a non-centered target, but that is not discussed in this article.  A normal distribution with a centered process is shown, figure 1.

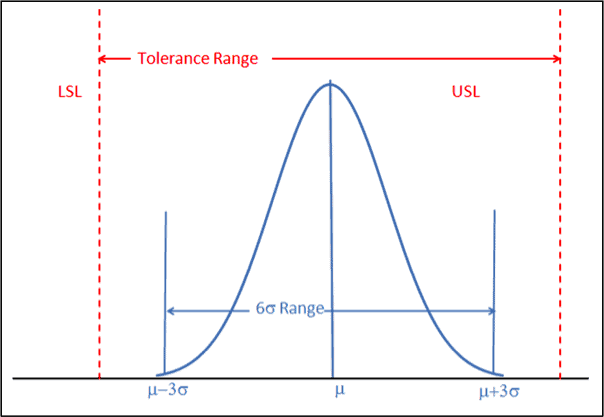
Figure 1

The ratio of the tolerance range to the 6s range is calculated in equation 6.

$$\frac{USL-LSL}{6\sigma}$$

(6)

If prototype parts were used to estimate $-\mu-$ and $-\sigma-$,

then the ratio in equation 6 is called the Process Performance, P_p. Alternatively, if SPC samples from a series process were used, then the ratio is the Process Capability, C_p.

There are three cases for centered normal processes with a 2 sided-tolerance specification, figure 2.

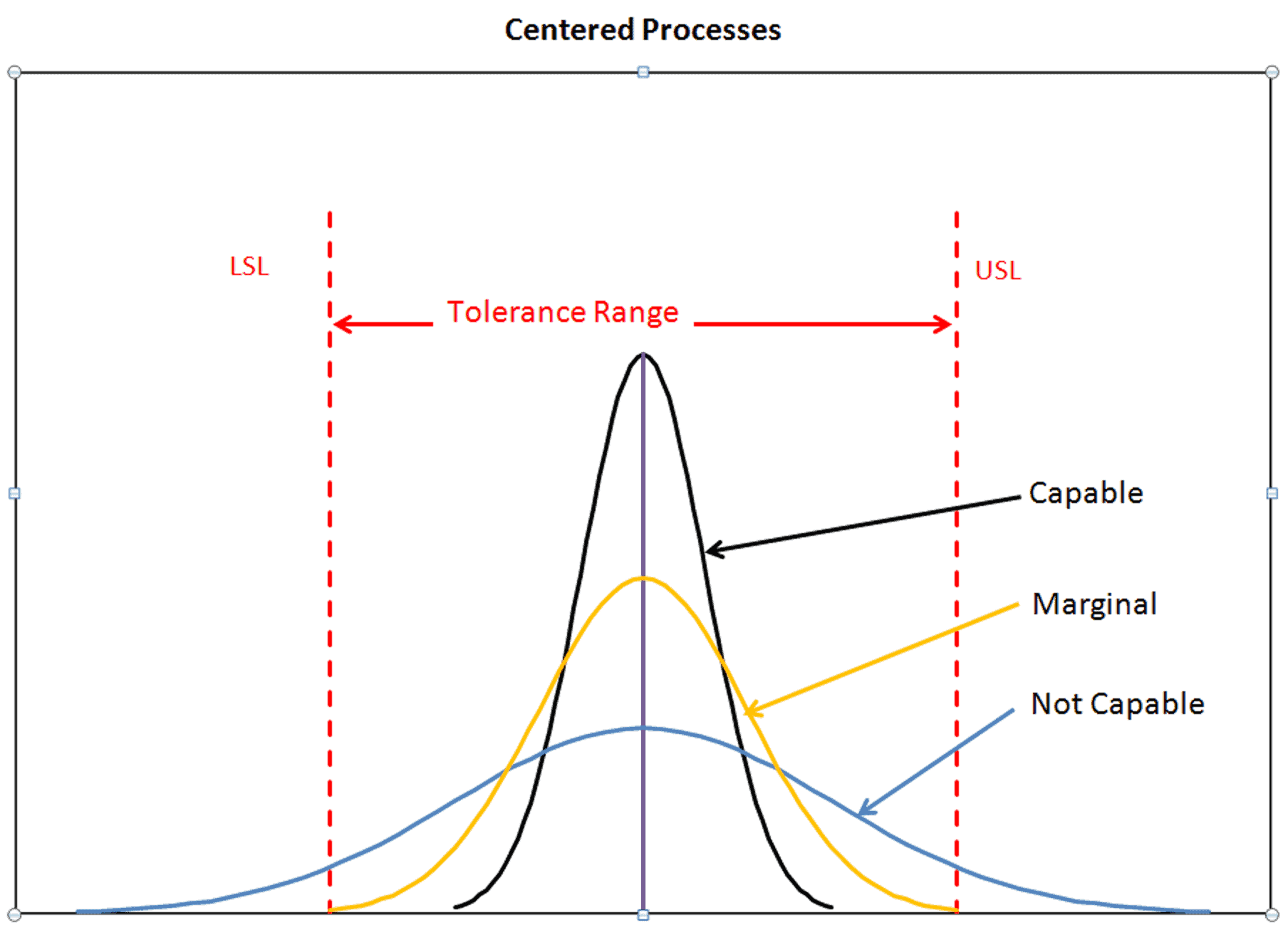
Figure 2

The greater the variation, the harder it is for a process to be capable. A capable process shown in black is within the tolerance limits and has a Cp (or Pp) = 1.67! A process that is not capable is shown in blue, has a Cp = 0.67. The distribution tails cross the specification limits, allowing the production of non-conforming parts. The marginal process shown in yellow has 3$-\sigma-$ distribution limits that just touch the tolerance limits. The marginal process Cp = 1. In marginal process, any change in the process average causes a tail of the distribution to cross the tolerance limit, allowing for non-conforming parts to be produced.

Some corporations target $-P_p\geq{1.67}-$ and $-C_p\geq{1.33}-$! Six Sigma practitioners target $-C_p\geq{2}-$, for a process under statistical control.

Non-centered Processes

The best performance comes from a centered process. A non-centered process produces more defectives than a centered process. Consider three distributions with the same spread, but different centers in figure 3.

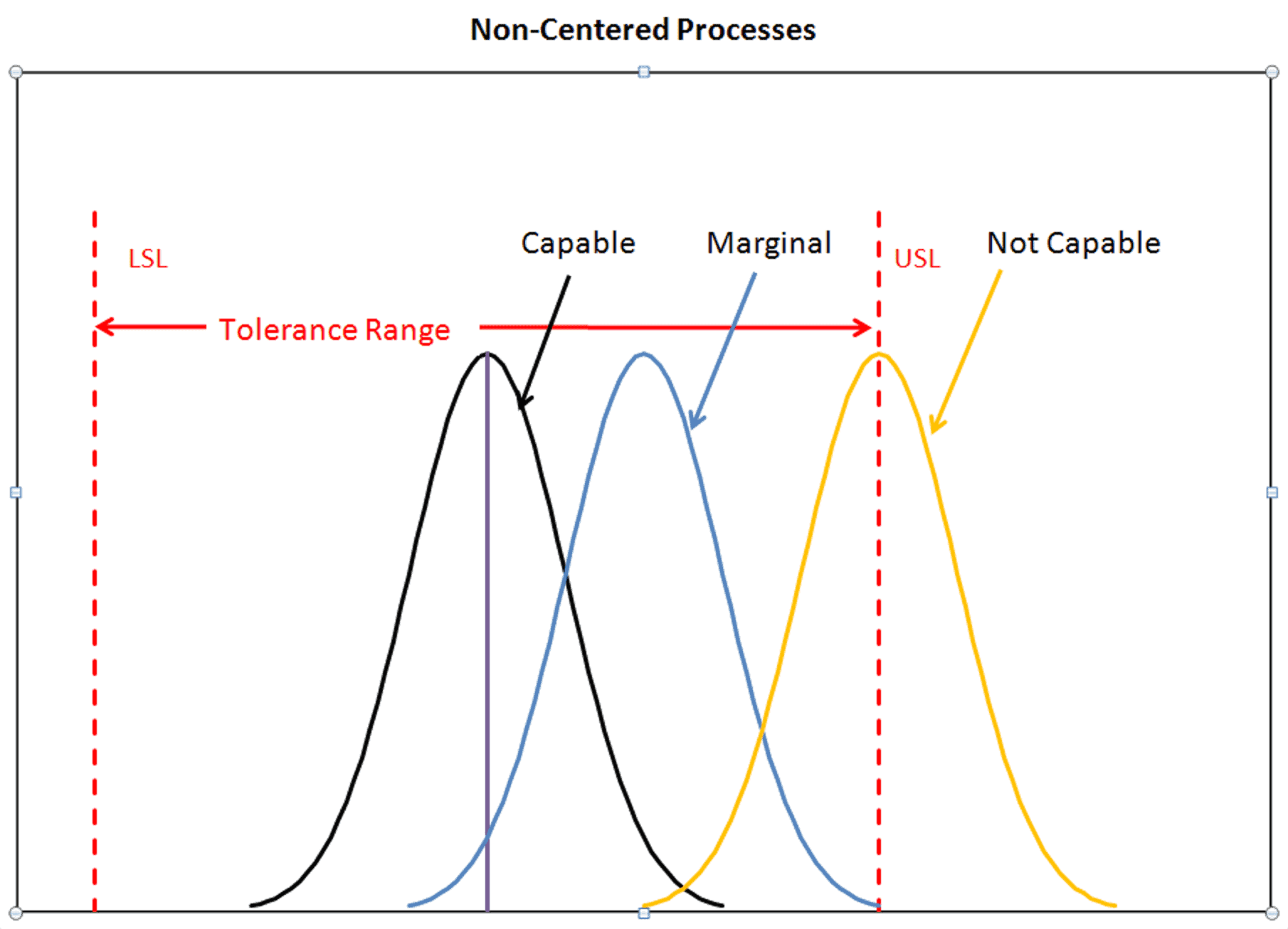
Figure 3

Here the process represented by the black distribution is capable; the blue distribution, marginal; and the yellow distribution, not capable. The process described by the yellow distribution produces about 50% non-conforming for the measured characteristic.

The gap between the closest tolerance limit and the center of the distribution is divided by 3$-\sigma-$ and captures the centering effect, figure 4.  and equation 7.

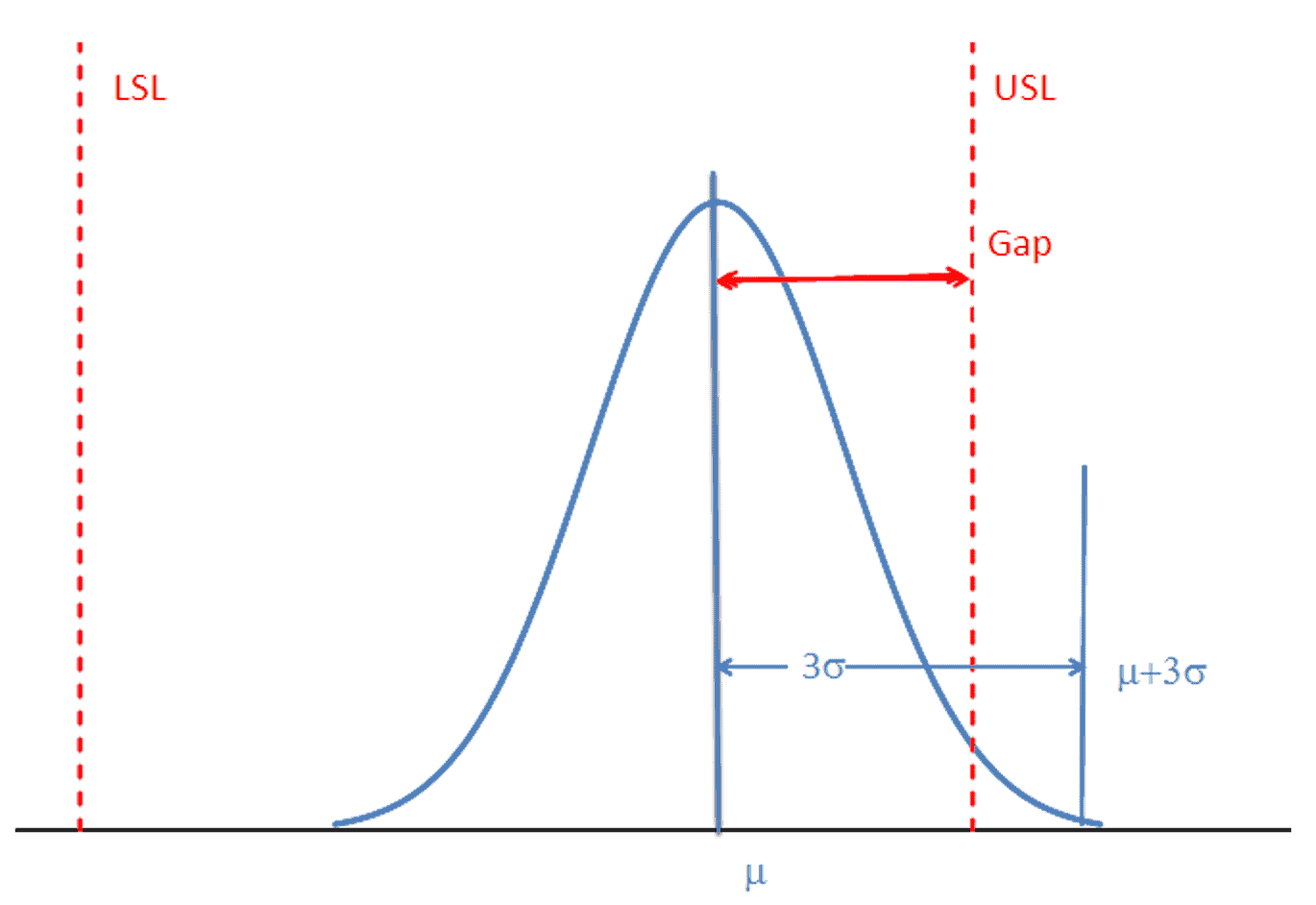
Figure 4

$$\frac{min(USL-\mu,\mu-LSL)}{3\sigma}$$

(7)

If prototype parts were used to estimate μ and σ, then the index, calculated in equation 4, is P_pk. If the data came from series production, then the index is C_pk.

If the 6$-\sigma-$ range is much smaller than the tolerance range, then the process center can shift but remain capable. If the 6$-\sigma-$ range is equal to or larger than the tolerance limits, then the process is not capable and needs to be improved. Identifying and controlling factors that contribute to process variation can accomplish this, but this is a topic for another article.

For a capable process, the indices P_p, P_pk, C_p, and C_pk, must to be greater than 1. For pro-type parts, some organizations want both P_p and P_pk, to be greater than 1.67! Because series production should include all sources of variation, some organizations want C_p and C_pk to be greater than 1.33!

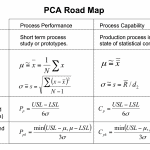
PCA Road Map 

These concepts, for two sided tolerances can be captured in a PCA Road Map in table 1.

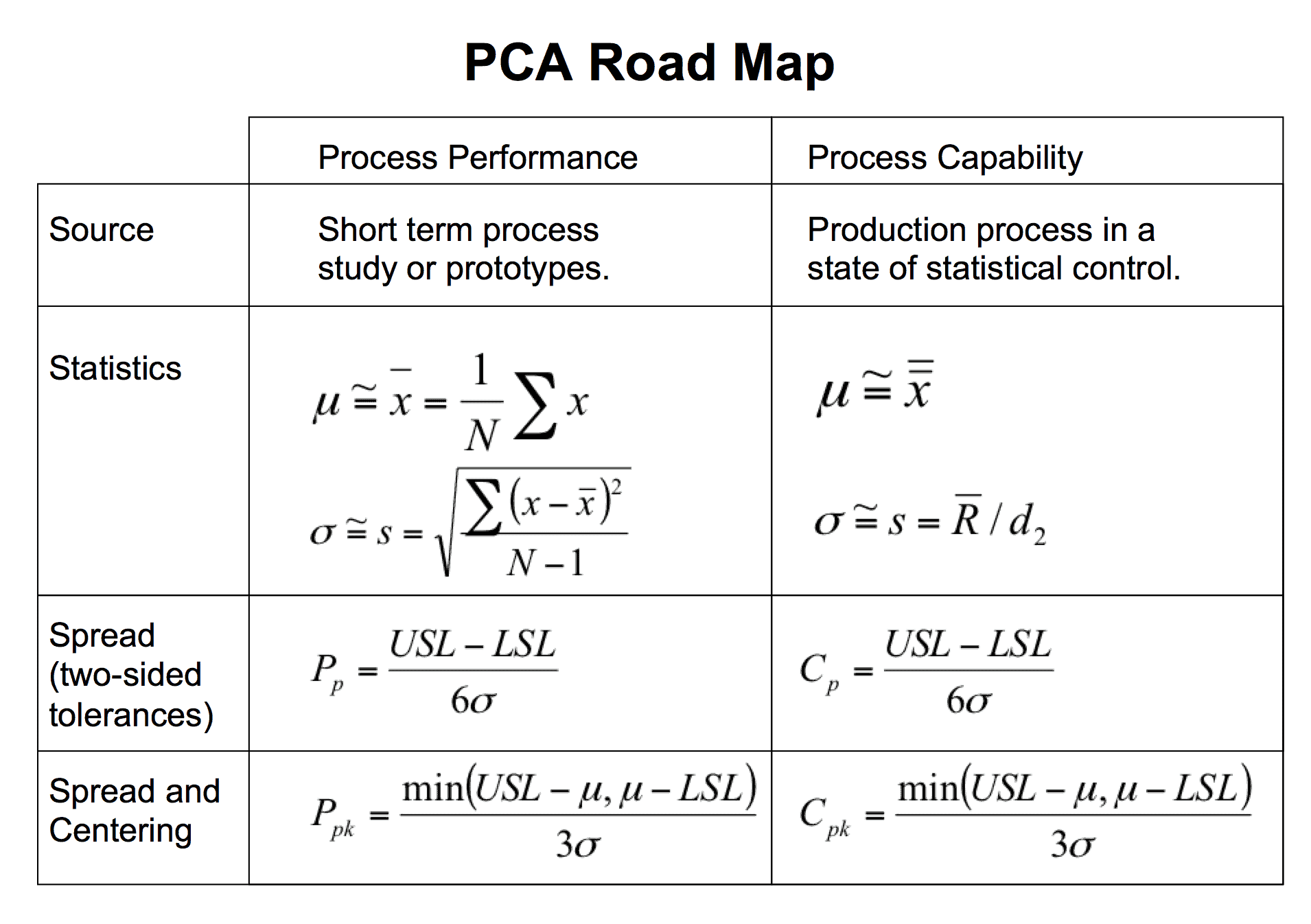
Table 1

Note the different statistical calculations in the second row. Both are recognized methods of estimating the mean, μ, and standard deviation, σ. In the second column, the source is a small sample of prototypes. In the third column, the source is production SPC.

One-sided Engineering Specifications

Some engineering tolerance are don’t have both an upper and lower specification limit. Frequently, physical constraints do not permit negative values. Some examples are surface roughness, wheel or tire radial run-out, the electrical resistance of electronic switches.  In these situations, only an upper specification limit is necessary.

In this situation, the tolerance range is unbounded on the undefined limit. It is not possible to calculate a P_p or C_p index. However, the P_pk and C_pk indices can be calculated using equation 7 with the defined specification limit.

Conclusions

A process capability analysis can determine if a process is capable of producing parts that conform to engineering specifications. While prototype parts can provide preliminary process performance information, the final process capability assessment must be based on series production.

The final capability index is highly dependent on the process being centered between tolerance limits and variation needs to be smaller than the tolerance range.

Next

The next article discusses how to estimate Percent Defectives.

Note

If you want to engage me as a consultant or trainer on this or other topics, please contact me. I have worked in Quality, Reliability, Applied Statistics, and Data Analytics over 30 years in design engineering and manufacturing. In the university, I taught at the graduate level. Also, I provide Minitab seminars to corporate clients, write articles, and have presented and written papers at SAE, ISSAT, and ASQ. I want to assist you.

Dennis Craggs, Consultant
Quality, Reliability and Analytics Services
810-964-1529
dlcraggs@me.com