The Arrhenius Equation is widely used and accepted by reliability and validation engineers from many industries to develop accelerated life tests (ALT) for thermal aging environments.
The general form of the equation describes the reaction rate of a process as a function of temperature (K), the Boltzmann constant (8.617E-5 eV/K) and two empirical factors. It can be written as:
$$ \displaystyle\large time=Ae^{\left\{ \frac{-E_{a}}{kT}\right\} } $$where Ea is activation energy (eV) and A is a proportionality constant.
A useful form of the equation relates time to failure on an accelerated test to time to failure under normal conditions:
$$ \displaystyle\large t_{a}=t_{n}e^{\left\{ \frac{-E_{a}}{k}\left[\frac{1}{T_{a}}-\frac{1}{T_{n}}\right]\right\} } $$where $- \frac{t_{n}}{t_{a}} -$ is the test acceleration factor AF.
This equation is often used when developing an aging test aimed at reproducing the thermal damage experienced in the field. It is also used to relate a new (accelerated) test to an accepted nominal test.
What makes this form of the equation powerful is that the proportionality constant has dropped out, leaving only the activation energy, Ea as the unknown parameter. As with all empirical factors, Ea is best determined experimentally but since it is highly material dependent, approximate values can be found from reference materials.
EXAMPLE:
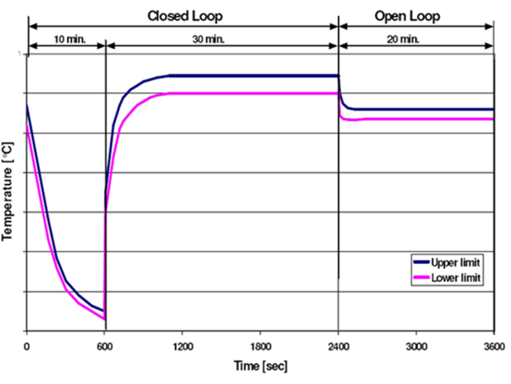
Not every field application runs predominately at a single high temperature condition. The figure at right is an example of automotive exhaust temperature measured on a repeating one-hour engine dyno test profile. The standard “one life” protocol is to run exhaust components on this engine profile for 2000 cycles or 2000 hrs.
Let’s say we are interested in creating an accelerated version of this test that runs on a natural gas burner at a constant 1000C and provides the same “thermal damage” as the engine dyno test, how would you do it?
One method is to split up the one-hour cycle into discrete bins and calculate thermal damage for each. We would then sum these values to represent the total thermal damage imparted by the full cycle.
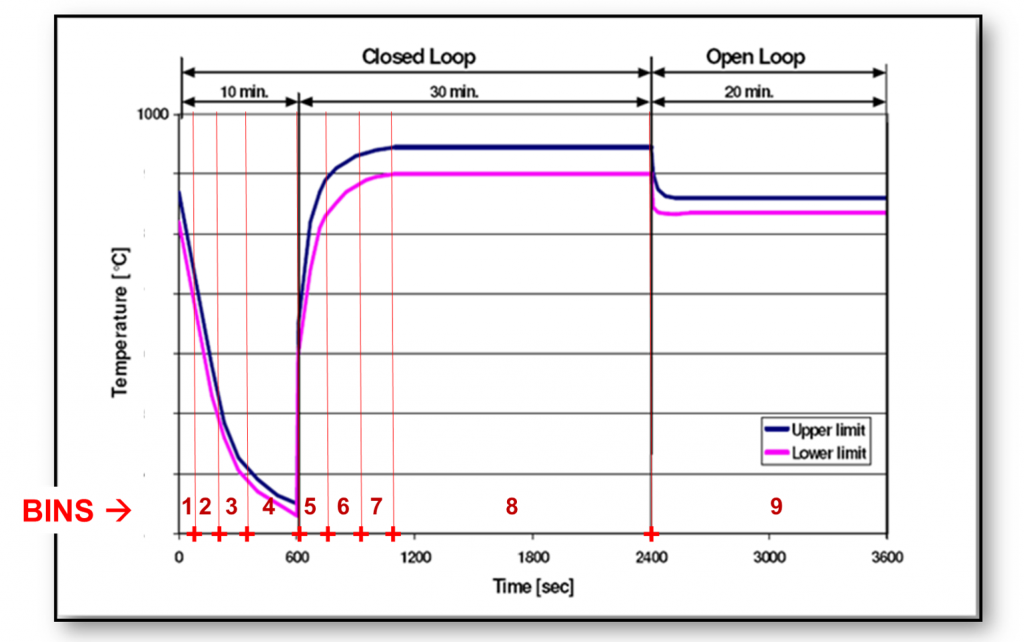
We define thermal damage for this purpose as the value of the empirical constant A:
$$ \displaystyle\large \textit{Damage}_{i}=A=\frac{t_{i}}{e^{\frac{E_{a}}{kT_{i}}}} $$A sense check confirms that damage increases with both temperature and time. The damage calculation for this cycle is an Excelexercise that would look like this:
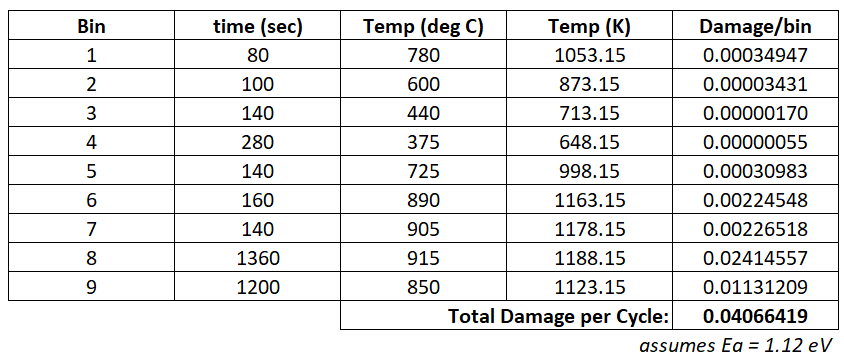
The total thermal damage imparted by this test would be 2000 cycles x 0.04066419 = 81.3328 damage units.
From here it is a simple matter to solve for the total number of hours required to run a constant 1000C burner test:
$$ \displaystyle\large Damage=81.3328=\frac{t}{e^{\frac{E_{a}}{kT}}}=\frac{t}{e^{\frac{1.12}{8.617E-5\times1273.15}}} $$or t = 614 hrs.
The result is an accelerated thermal aging test that runs on a burner at 1000C for 614 hrs, imparting the same thermal damage as the engine dyno test that runs for 2000 hrs.
There are a number of caveats/assumptions that must be considered:
- The elevated temperature chosen for the accelerated test must not introduce failure mechanisms that are not observed on the nominal test.
- It assumes that thermal aging damage is cumulative.
- A steady state thermal aging test will accelerate failures related to thermal degradation. However, it does not contain thermal cycles and thus does not induce thermal fatigue failures that may be important. It also does not contain engine exhaust gasses so it would not induce failures that rely on these constituents.
- The temperature value chosen to represent each bin could be the maximum (conservative) or midpoint, though this becomes less important as the number of bins increases.
- Actual damage units are unimportant. What is important is to be consistent with the units that are used.
* Excerpted from Reliability Alliance training: Introduction to Reliability Engineering & Accelerated Testing
Leave a Reply