Definition of a PF Curve
A PF curve is a graphical tool used in the field of maintenance and reliability. It essentially illustrates a component’s health degradation over its lifetime. As well as a visual guide on when to conduct appropriate action to minimizes operational risks related to unplanned failures. It is essentially a planning tool.
The PF Curve is a combination of Condition Based Monitoring (CBM) tasks and Repairs (or Corrective Maintenance) tasks. Below is a classical PF curve with asset consumed life on the horizontal axis. The asset starts operating at time zero. The vertical axis indicates the health or the condition of the asset at a specific moment in its life. When we install or commission the system at time zero, the health index is close to or at 100%. As we move away from time zero, the condition typically degrades and the health index decreases. When the asset is at its end of life, the health index is close to or at zero.
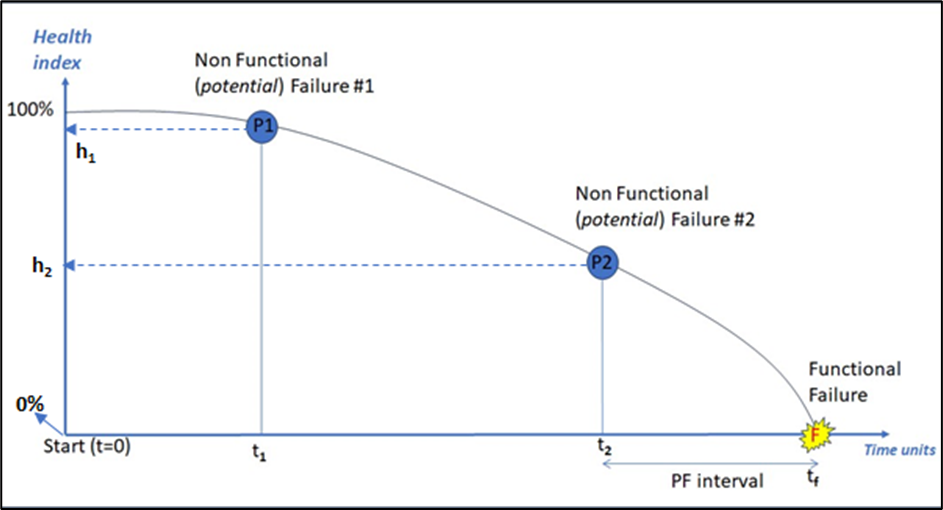
In the PF acronym, P stands for Potential (related to a failure) and F for Functional (also related to a failure). A potential failure or non-functional failure means that the asset is showing initial signs of degradation yet still performing its function. CBM procedures detect non-functional failures. Such as Vibration, Infrared or Oil Analysis. Human senses cannot detect those degradation thresholds. A functional failure is when the asset losses is function completely. A typical functional failure is obvious to the operator. A repair task usually follows.
Using the PF Curve
One of the most important outputs of a PF curve is what we call the PF interval. In Graph 1 above, it is the time interval tf minus t2. This is the time from an advance degraded condition (P2 here) to the time we lose total function of the asset (F). Note, that we could equally have used P1 as the reference point. F can also be qualified as the “end of life” stage.
The PF interval informs the operator after reaching the detectable degraded condition, in this case P2, how much time they have left to mitigate the total failure of the asset. We want to avoid reaching the F point. Mitigation will be a planned repair which is shorter and more controlled. If we reach the failure point without mitigation, we end up with an unplanned failure with many adverse consequences for production, employee safety as well as high repair costs.
The PF interval is crucial because, if the repair is a complex or costly job, the PF interval gives the operator time to plan and budget for the repair. These include preparing for production downtime, getting spare parts and having a repair plan ready. Note that the mitigative action could be a repair, a restoration task or it could be entirely replacing the asset itself. Therefore, the PF interval is very useful to an operator who has a large number of assets to manage and maintain but has limited maintenance resources to execute the work. The correct PF interval will allow for planning and execution of all the required repairs in an optimized schedule. This also avoids repairing too early which is costly, or repairing too late which is risky.
Defining the PF point using Life Analysis
In general literature it is not clear how to build PF curves. Specifically, the time intervals for the P and F points. Is Mean Time Between Failures (MTBF) used? Or is it something else?
I prefer to use Life Analysis as a more rigorous approach. Life Analysis involves using degradation records to build a statistical life model. In the case of a 2-point PF curve (i.e. one P point and one F point), we will have to build 2 statistical models. One for the CBM degradation threshold (P) and the other for the functional failure (F). Therefore, we need two sets of degradation records. Those life models take into account the true evolution of the component degradation.
The question now comes to: how are the P and F point defined using those life models? It depends on the analyst. It can either be the characteristic life value or the scale parameter if the model derives from a Weibull distribution. One can also define a probability of event occurrence time value. For example, the time where we have 90% probability of degradation or failure. And again, both for the P and F points.
Here is a real life PF curve example below presented at LRVS AMERICA 2024.
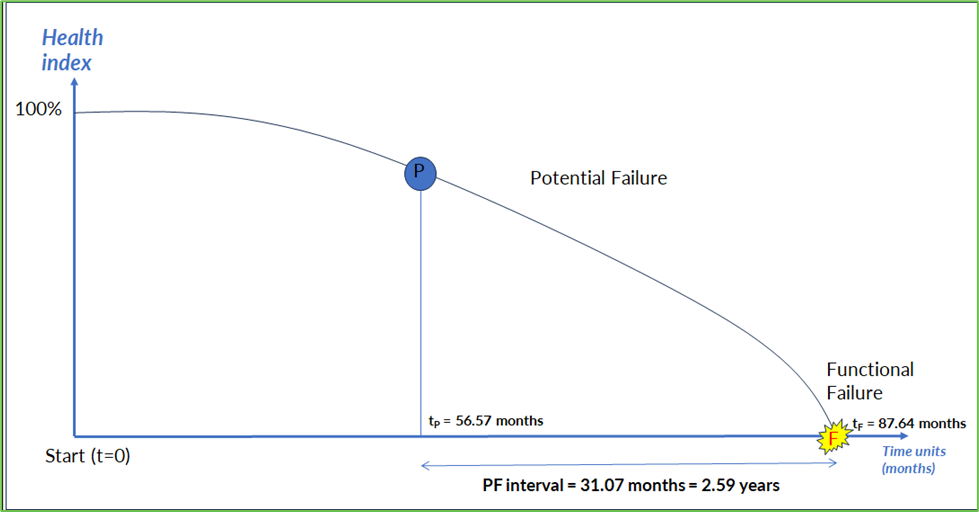
The example relates to roller bearings where we use Vibration Analysis as the CBM method. Two degradation models are defined for the P and F point respectively as follows.
- P point: Weibull 2 parameter distribution: Beta (shape parameter) = 1.43; Eta (scale parameter) = 56.57 months
- F point: Weibull 2 parameter distribution: Beta (shape parameter) = 1.62; Eta (scale parameter) = 87.64 months
In this case, we use the Characteristic Life (Eta) as the P and F points. The PF interval as shown in Graph 2 is 31.07 months or 2.59 years.
The reader will notice a glaring omission in Graph 2. The graph does not specify nor illustrate a health index for the P point. It is omitted because what is of interest to the user is the PF interval. The health index value does not allow for any decision making in this case. It can be back calculated using the ratio tp/tf.
In summary, the question becomes: is the PF curve of any value to the maintenance and reliability practitioner? Since the PF interval happens to be the most important element and can be calculated separately. Comments from the readers on the above question are more than welcome.
Leave a Reply