
This simple example explains how to calculate the failure rate of parts, known as the Hazard Rate, using a drinking glass. Historic records, like maintenance, operating, supply chain, and financial information, are accessed to understand the situation being analyzed and gather modelling data. Once all necessary information is collected and the situation is investigated, then proposals to address and solve the problems causing and permitting the failure to happen are selected and a business case is developed.
Reliability engineering is a branch of statistics and probability that is used to calculate the failure rate of machines and parts. A reliability engineer uses historic records of failure events to develop a failure rate curve of an item. Failure rates are fundamental in reliability analysis.
In the image below, a drinking glass is used as an example component. Explosions mark when a glass was broken and a are color-coded by the reasons they broke. The orange box lists 15 potential causes of glass breakage. This includes dropping, knocked, crushed, shocked by temperature and vibration, they can be mistreated, and they can succumb to previous damage.
For this example, we will assume that a million of a particular type of drinking glass and were made and sold in packs of 12 from stores around the world. The packs of 12 were purchased by individual households, which means that 83,333 homes used the glasses.
Each household is different, and so carries its own hazard risk. Houses with only one adult living it in will have a lower Hazard Rate. Houses with more people in a house, the more times the glasses are used and a higher Hazard Rate. Those with young children and elderly people carrying a greater risk of glass breaks. In this situation, we will assume that a “typical household” has an average of two glasses broken a year.
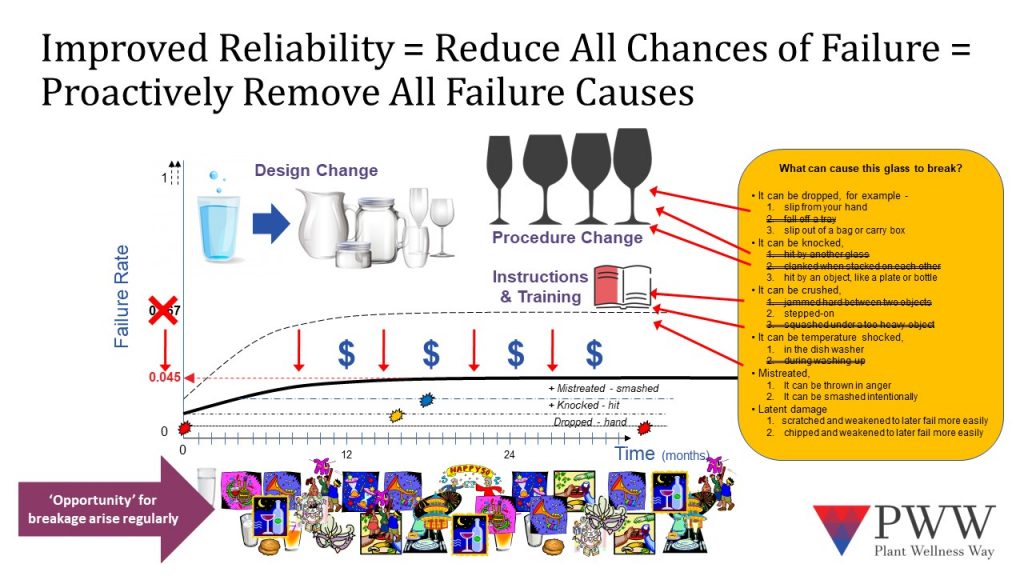
Before a failure event there first must be an opportunity for a glass to be used. Each glass in the pack of 12 started its service life by being removed from the wrapping and put onto a shelf. At time zero the failure rate will not be zero, because with nearly 1,000,000 opportunities to be broken, some glasses will not make it from the pack to the shelf. So, the failure rate curve for our “typical household” begins at a point slightly above zero to allow for the occasional early life failure. The remaining glasses will not fail until they are broken by some event that happens during their lifetime. Acts of nature are excluded from this basic example.
Along the bottom of the plot are situations and events where glasses are needed. Each use is an opportunity for a glass to be broken. Among the population of 83,000-plus households’ glasses will be broken every day.
Initially the failure rate will start to climb as each month goes by and more opportunities occur for a glass to be used. By the end of 12 to 18 months the range of opportunities will repeat. Annual events will re-occur, occasional random uses of the glasses will arise now and again. In time, a reasonably constant set of opportunities tend to reoccur in each household. If all homes were a “typical household,” then each year on average about 166,667 glasses around the world will be broken and replaced.
Because the failure curve becomes a line after about 18 months, we have a steady rate of breakage at 166,667 per million glasses, which is an average failure rate, or Hazard Rate, of 0.167. This Hazard Rate assumes that each broken glass is replaced after breakage to keep the usable population at a million glasses. This approach is a simple example of determining the failure rate curve of an item in a stable population of items.
If the failed glasses are not replaced, then the population shrinks by 166,667 annually. Because the opportunities to use glasses are reasonably consistent each year, the number of glass breakages will remain at the “typical” level year to year. In the second year of our “typical” two-glass-breakage-per-year household, another 166,667 glasses will be broken world-wide. But since the initial population was 833,333 (1,000,000 – 166,667). The Hazard Rate would then be 0.2 (166,667 / 833,333). Each year the Hazard Rate would rise as the remaining population decreases.
As we can see from this example, it is best to model your own failure data. To do that you must have impeccable historic records of when your items failed, and the history of how they were failed. The unfortunate truth is that hardly any company in the world collects failure data to that level of detail. And so, Reliability Engineers must make assumptions and build some sort of model, even though the model will not be a true reflection of reality.
 Ask a question or send along a comment.
Please login to view and use the contact form.
Ask a question or send along a comment.
Please login to view and use the contact form.
“… it is best to model your own failure data. To do that you must have impeccable historic records of when your items failed, and the history of how they were failed. The unfortunate truth is that hardly any company in the world collects failure data to that level of detail.”
Companies don’t need life data by item name or serial number for each product or its parts (or even a sample), to make nonparametric estimates of age-specific field failure rate functions, without unwarranted assumptions, for all its products and their service parts. Periodic ships and returns counts data required by GAAP are statistically sufficient.
Thanks to Fred for publishing:
https://accendoreliability.com/field-data-reliability/
https://accendoreliability.com/firestone-tire-reliability-circa-year-2000/
and a some more of my articles explain:
Revenue=ships*Price per unit shipped
Warranty or service cost = service cost*number of complaints, part services, or spares consumption.
I admit, it takes work to extract periodic ships and returns counts. It also takes gozinto theory and BoMs to convert product installed base into parts’ installed base by age. It takes statistics to convert ships and returns counts into nonparametric estimates of failure rate functions. Then you can compare the cost of a little work on GAAP data with the cost of tracking the life every product or part, or even a sample.