
Introduction
Quality Costs for manufacturing or services can be categorized as prevention and appraisal costs, and internal and external failure costs. Control occur in prevention and appraisal activities, both of which rely on data. However, when data is collected, it shows variation. One must understand variation to know how to react.
Dr. Deming indicated that 94% of variation is from common causes and about 6% is from special causes. So what are the common and special causes of variation?
Common Causes
Common causes of variation are inherent to a system. Services are subject to variation. In a bank, different transactions and customers require different amounts of time. There is part-to-part variation for items being manufactured. The part characteristics show variation. The assembly of automobiles, planes, and other product show to variation. Common cause of variation is inherent to the system.
When a product or process characteristic is repeatedly measured, it may be analyzed with a histogram. If the data shows a “bell” shape, it may be normally distributed. The data is clustered about a central value and the clustering is called variation. If more complex patters are shown, such as multiple peaks in the histogram, then some further analysis is required. If the histogram is truncated, there may be some in-process sorting occurring. If some measurements are prohibited by physics, then other non-normal distributions need to be considered.
Special Causes
Special causes of variation are due to factors that perturb the system. Something happens to disturb the process. For example, my drive to work takes time. An expected amount of drive time could be stated as an average plus or minus some variation. However, this process is subject to delays, i.e., a vehicle accident, road construction, very heavy or light traffic, bad weather conditions… What should be a 30±5 minute trip becomes a 2-hour trip. These are special causes at work.
In manufacturing, special causes may be found in manpower, materials, machinery, measurement equipment, or the environment. For example, the purchased power for a plant can experience voltage dips, especially on hot days when other customers are running their air conditioning. A new employee may need training. A material supplier may be added. The special cause may be hard to identify.
Reacting to Variation
A process may be stable for a time, but then the data shifts. The question remains as to how big of a change is important? Should one ignore the change or react by adjusting the process? Consider the truth table for this situation.
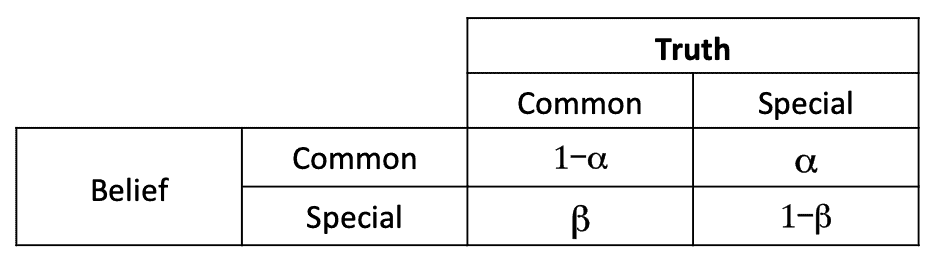
Table 1
Suppose our belief is that only common causes are creating variation and this belief leads to a decision to do nothing. If the reality is that a special cause happened, then our decision allows an out of control condition to continue. Let $-\alpha-$ be the probability of making this error. Then $-1-\alpha-$ is the probability of being correct.
If our belief is that a special cause is responsible for the variation, then that belief leads to some action. If the reality is that only common causes of variation existed, then the action may increase variation. The action becomes a special cause. Here, $-\beta-$ is the probability of making the error and $-1-\beta-$ is the probability of being correct.
Our decision rules need to minimize the $-\alpha-$ and $-\beta-$ probabilities
The Funnel Experiment
Dr. Deming created the funnel experiment to evaluate different strategies for controlling a process subject to common causes. In this experiment, a funnel was positioned over a target and a marbles dropped through the funnel. The x and y position of each marble impact relative to the target was noted. He evaluated different reaction strategies.
Rule 1: Do nothing
Rule 2: Adjust the funnel location by the x and y distance to target of the last marble dropped.
Rule 3: If the last marble missed the target, shift the funnel location relative to the target.
Rule 4: If the last marble missed the target, position the funnel over the last impact point.
Rules 2, 3, and 4 are not the best strategy since they are based on the last marble dropped. This strategy ignores the inherent common causes and over controlled the process. In the experiment, the marble impact points showed more variable and miss the targets worse than Rule 1.
A better strategy is to collect the data using Rule 1. When sufficient data is collected, perhaps 30 samples, the average and variation inherent in the system, i.e., common cause variation, can be determined and the funnel position corrected. This and other approaches will be discussed in future articles on Statistical Process Control.
Conclusion
We need to develop a strategy that allows us to distinguish common and special causes of variation. Dr. Deming’s funnel experiment shows that using the wrong reaction plan can make a process worse. Fortunately, statistical process control provides tools that meet this objective.
Note
If anybody wants to engage me as a consultant or trainer on this or other topics, please contact me. I have worked in Quality, Reliability, Applied Statistics, and Data Analytics over 30 years in design engineering and manufacturing. In the university, I taught at the graduate level. Also, I provide Minitab seminars to corporate clients, write articles, and have presented and written papers at SAE, ISSAT, and ASQ. I want to assist you.
Dennis Craggs, Consultant
Quality, Reliability and Analytics Services
810-964-1529
dlcraggs@me.com
 Ask a question or send along a comment.
Please login to view and use the contact form.
Ask a question or send along a comment.
Please login to view and use the contact form.
Leave a Reply