Introduction
An extended warranty is a prolonged warranty offered to consumers in addition to the standard and generally free manufacturer’s warranty on new items. It is also referred to as a service agreement or service contract, providing coverage for repairs or replacements after the manufacturer’s warranty expires. Extended warranties may be offered by the warranty administrator, retailer, or manufacturer, and they often come at an additional cost. Sometimes significantly in relation to the item’s base price.
The basis of this article is: should you consider buying extended warranty? What are the pernicious calculations it hides? It is often alleged that extended warranty is a ploy to extract more funds from a customer. Whilst this article does not question the honesty of the vendors of extended warranty, it demonstrates how warranty is calculated and that’s where the “devil” might lurk.
How is Warranty typically calculated?
It is actually a reliability calculation. In academic terms, Reliability is the probability that a system will perform its intended function in a specified mission time. For example, what is the probability that the pump will pump fluids without failing for a period of a year. Conversely what is the probability that it will fail in the same mission time of a year?
The mission time is thus a key consideration in the above definition. As it is in warranty calculations. What is the probability that the commodity will fail within the warranty period or mission time? It is in the interest of the vendor that this probability is very low or better, nil. So, it is important to calculate this specific mission time.
Example of Warranty Calculation
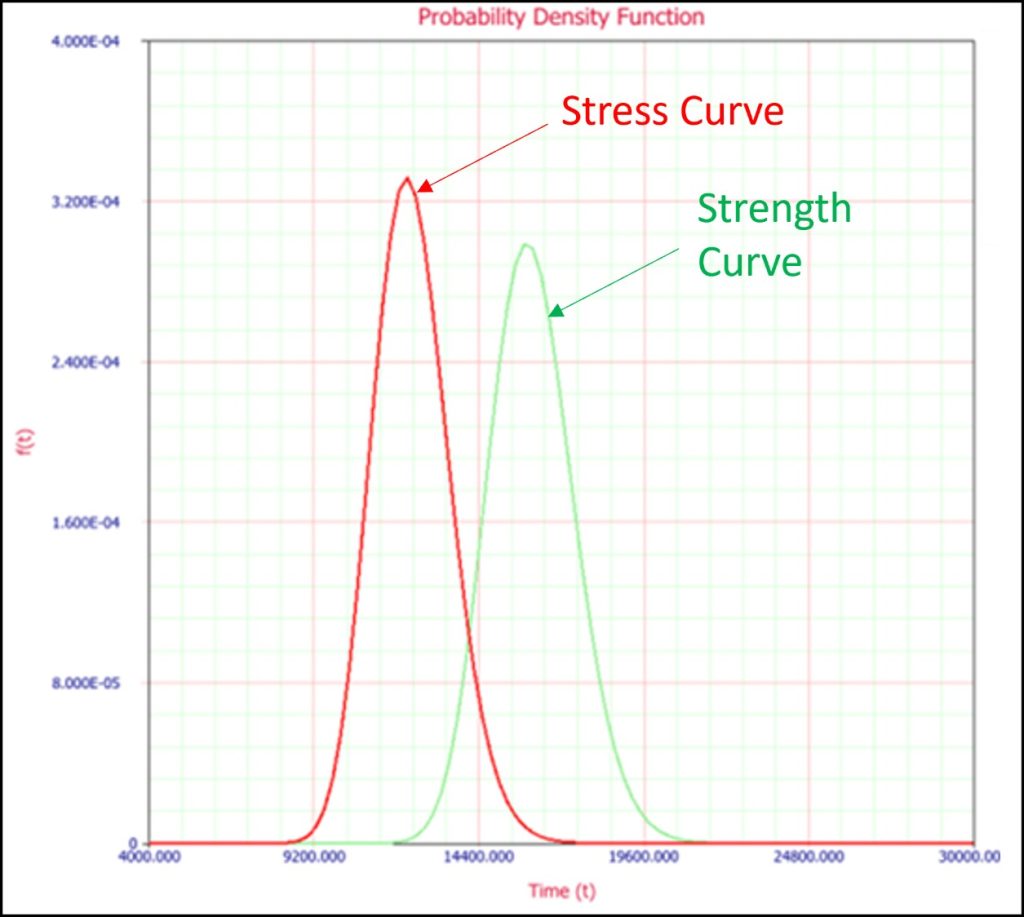
The example below uses the Stress-Strength analysis process and is provided by Reliasoft®.
A Stress-Strength analysis is used to estimate the reliability of an automobile component. The stress is defined by the automobile yearly mileage records. In other words, driving the automobile causes mechanical stresses and therefore degradation. The strength is the miles-to-failure distribution. Two life models as shown in Graph 1 below, represent the Stress-Strength analysis. Both are lognormal distributions and the best fits for the data provided.
The standard manufacturers warranty is required to be 1 year or 15,000 miles, whichever is earlier. The goal is to estimate the reliability of the component within the warranty period of one year or 15,000 miles which ever comes first.
Based on the above distributions, the estimated reliability for this automobile driving 15,000 miles or less per year is 98.84%. Conversely the probability of failure is 1 minus 98.94% thus equal to 1.08%. Which is a very low probability of failure. Therefore, it would be in the advantage of the warranty provider to set the warranty limit at 15,000 miles or 1 year.
Just as an example, if an extended warranty package is offered for an extra 25,000 miles or an extra two years whichever comes first. This means that the extended warranty time limit would be either 40,000 miles or 3 years. The calculation shows a component failure probability of 22.27% which is much higher. But possibly low enough to be in the advantage of the manufacturer. Additionally, the cost of this extended warranty will also be factored, in relation to the higher risk of failure.
Conclusion
The reader of this article is now armed with improved knowledge in terms of how warranties are calculated. Behind every warranty offer, “hides” a Reliability Engineer doing the math on what is the best commercial outcome for the vendor. As a matter of fact, warranty and warranty calculations are a fundamental part of the Reliability Engineering discipline.
Leave a Reply