Machine Vibration Isolation – Theory and Practice

1. Application.

Any engineer with known expertise or responsibilities in the area of ‘vibration’ will be asked sooner or later to advise on a vibration isolation problem. While the principles of vibration isolation are relatively simple to understand the practical application requires some design skills and a good understanding of the vibration source or sources.

Vibration isolation problems can be divided into two main groups.

Firstly, the need to reduce the transmission of vibration from a machine to the structure supporting it. Examples are, the isolation of the engine from the chassis in a motor vehicle; isolation of mechanical services equipment (eg fans and chillers) in hospitals and commercial buildings; isolation of noisy pipework from masonry structures, and isolation of vibrating screen decks from the screen house structure. As we will see, these applications are usually solved fairly simply and with readily available isolation products.

The second group is the reverse of the above – the need to reduce the transmission of vibration from a vibrating structure to a machine or some equipment supported by it. Generally these are much harder problems to solve due to the relatively low frequency source vibrations generally found in structures. Examples are, the isolation of the drivers cab on an earthmoving machine; the isolation of a precision instrument (eg microscope) from common building vibrations; isolation of sensitive electrical equipment from excessive building vibrations (e.g. a screen house), and the isolation of a motor vehicle from the roughness of the road surface.

There is a third related group that comes under the heading of ‘vibration minimisation’ or ‘damping’ rather than vibration isolation. We will only look briefly at these applications.

2. Displacement and Natural Frequency.

The fundamental rule of isolator selection can be stated as follows:

‘The natural frequency of an isolation system is in proportion to the linear deflection of that system from the unloaded state’.

There are a number of conditions and limitations for the application of that rule but, for all practical selection purposes, it holds true. This rule derives from the equation defining the natural frequency of a single degree-of-freedom, undamped mass-spring system.

$$ \displaystyle\large f_{n}=\frac{1}{2}\pi\sqrt{\frac{K}{M}} $$

Assuming that, for a given system, mass is a constant then fn is proportional to the square root of stiffness, or inverse to the square root of deflection.

Refer to the Isolation Efficiency chart at the end. You will note that the vertical axis of the Chart lists both Natural Frequency and Static Deflection. The natural frequency for a system with a static deflection of 100mm is approx. 1.5 Hz whereas a system with a static deflection of 25 mm is 3.0 Hz. The ratio of the deflection square roots is 2:1 and the frequency is inversely proportional.

We will now consider some practical applications of vibration isolation design and selection.

3. Reducing Force Transmission from Machine to Structure.

The starting point is to determine the lowest forcing frequency of the machine. Usually this is determined by the lowest shaft speed in the machine because of the potential residual unbalance of that component.

The next consideration is the quality of isolation needed. If noise is the dominant consideration then the system will almost certainly use rubber as the isolation medium because of the excellent isolation it offers to the higher (audible) range of frequencies. If vibration is the main concern then almost certainly springs or some form of soft suspension will be employed to provide isolation at relatively low frequencies.

The location of the isolator elements must then be considered together with the considerations of stability and integrity under all possible load or shock conditions.

It is critically important to ensure that all isolator elements have the same deflection. Many machines are heavy at one end and it will be necessary to provide elements with a higher stiffness to support the heavy end of the machine. The object is to produce a level machine with the same deflection on all elements and hence the same mounted natural frequency at all points of support.

The following classic mistakes are often made in the design of isolation systems.

• Lack of Base Rigidity. If the base frame of (say) a motor-pump set is going to be mounted on isolators then the frame itself must provide all the stiffness necessary to maintain static alignment plus the driving torque. Short coupling life on an isolated machine is a certain indicator of inadequate base stiffness.
• Mounted Natural Frequency Too High. Relatively light machines (such as small fans) are often found to be mounted on isolators that have been selected with an eye to stability rather than isolation. The result may be that vibration on the machine itself is amplified and the isolation effect is greatly reduced.The required solution here is an Inertia Block to provide added mass and stability. Quite often the base frame is fitted with a sheet metal bottom and the whole frame filled with concrete. It has the bonus of added torsional stiffness as well as greatly improved isolation dynamics.
• Introduction of Rocking Modes or Instability. The engine of a motor vehicle is required to be held stable over a wide range of dynamic conditions and therefore isolation design includes ‘captive’ isolators that are able to resist forces in all directions. Simple isolators that have no significant strength to resist tearaway or overturning forces may be inherently dangerous.
• Other Natural Frequency Modes. There is potential to introduce natural frequencies in directions other than the principal direction of isolation when captive isolators are used and therefore the transverse stiffness and coupled mass must also be checked to ensure that the dynamics of the system will be satisfactory in all possible modes.
• Instability When Traversing Natural Frequency. Machines which have a relatively slow start-up or run-down pattern may well become very unstable as they traverse the mounted natural frequency range. Examples are large vibrating screen decks and centrifuges. The design must include consideration of limits to acceptable vibration amplitudes for these transient conditions.

4. Reducing Force Transmission from Structure to Equipment.

The solution of these problems generally requires a lot more careful consideration if a good outcome is to be achieved.

Structural vibration generally arises from machinery mounted on the structure that may have forcing frequencies from (typically) 12 to 25 Hz. This is commonly the case in minerals processing plants where crushers, screens and conveyor drives are often mounted on relatively flexible, high steel structures. Isolation may be required for operator comfort, electrical or instrumentation protection or to minimise false brinnelling of stationary machine bearings.

Problem: Let us consider by way of example a screen building vibrating at 12 Hz and this vibration is seriously affecting the reliability of switchgear and instrumentation in a control cubicle that weighs800 kg. A reduction of 80% of vibration displacement is required.

Solution:The Forcing Frequency here is 12 Hz. The commercial Isolation Efficiency Chart at the end of this paper shows that for a Forcing (Disturbing) Frequency of 720 CPM with 80% isolation we need deflection of around 10 mm and the mounted natural frequency will be about 5 Hz.

The upper table titled the Static Deflection Guide indicates that this is an application for 25 mm Deflection Springs. The deflection is too large for rubber.

An alternative solution may be to use airbag isolators which have better damping but will give a similar isolation efficiency.

Regardless of the solution chosen, there must be consideration of ‘live loads’ – such as several technicians being in the cubicle at once – and the potential instability of the system.

Where very low natural frequencies are required to achieve good isolation there will almost certainly need to be consideration of inertia bases to achieve the required mass and stability.

5. Dynamic Dampers.

The Dynamic Damper uses the inherent phase shift of resonance to provide a mass that will absorb energy from the vibrating system and thereby reduce amplitudes. Vibration minimisation by this method can only be considered for systems with a single frequency of excitation.At least one large city skyscraper in Sydney has the fire water tank on the top level mounted on springs so that its lateral natural frequency is the same as the first mode (simple cantilever)natural frequency of the building. When the building commences to sway at its natural frequency when excited by high velocity winds the water tank effectively moves in antiphase to the building and absorbs energy. The reduction in amplitude is said to be very significant.

The same principle is used on the sub-frames supporting the engine in some motor cars where several small masses (about 2 kg each) are mounted on rubber at the same natural frequency of the sub-frame. The result is a significant reduction in transmitted vibration and enhancement of the effectiveness of the vibration isolators connecting the sub-frame to the chassis.

Refer to the section in this manual on Phase Lag on Rotating Systems where the principles of phase shift are explained.

Appendix to Session. Isolation Theory.

The fundamental concern of the engineer seeking a vibration isolation solution is the reduction of transmitted vibration forces to or from one structure to another.

The isolating elements will typically be made of rubber or metallic springs. The transmitted force will be the instantaneous vector sum of the force transmitted through the spring component (proportional to displacement) and through the damping component (proportional to velocity) assuming that the masses of the spring and damper elements are collectively negligible compared to the mass that they support. Hence the term ‘transmissibility’ which is used todescribe the theoretical performance of a particular isolation application.

Curves showing the absolute transmissibility as a function of the frequency ratio f/fo for various damping ratios.

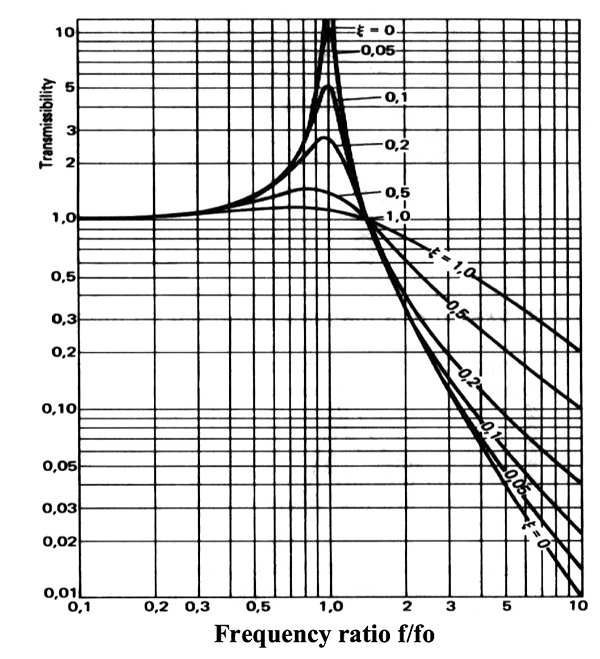
The set of curves given in the above figure convey a lot of information about vibration isolation. The vertical axis is the Transmissibility Ratio and shows values below and above 1.0 where the force into the isolating system is the same as the force out. The horizontal axis is the Forcing Frequency Ratio showing frequency ranges below and above 1.0 which represents the

The six curves supplied indicate the response for six different damping coefficients () ranging from Critical Damping ξ = 1.0 through to a theoretical ξ = 0.

The Transmissibility Ratio becomes theoretically infinite for zero damping but the isolation effect is very good for Forcing Frequency ratios as low as 2.0. However, this is obviously a very unstable system.

At the other end of the scale, systems with high damping coefficients (eg sports car suspension) have a much less efficient isolation effect but much greater stability across the whole range of excitation.

Isolation systems that use steel coil springs for relatively high displacements have low damping coefficients (typically ξ = 0.02) and, in the common case of motor vehicle suspensions, it is necessary to have dampers installed (so called ‘shock absorbers’) to provide stability.

Systems that use rubber isolators do not need separate dampers because rubber – and similar elastomers – has good inherent damping properties. However, the isolation efficiency is not so good and generally the range of displacements which can be accommodated are relatively small. Damping coefficients are typically ξ = 0.2.

Vibration Isolation Calculation

Problem:

The exciter in a vibrating screen rotates at 720 RPM (12 Hz). The building it is in also vibrates and the movement is seriously affecting the failure rate of switch gear and instrumentation in a control cubical mounted on the building floor. The cubical weighs 800 kg. A reduction in vibration severity of 80% is required.

Solution:

The Isolation Efficiency Chart advises that for a disturbing frequency of 720 RPM and an 80% reduction in vibration severity the frequency of the new arrangement must be about 5 HZ. This will require a 10mm static deflection of a supporting isolation system. The Static Deflection Guide indicates that this is an application for 25 mm deflection springs. The required deflection is just slightly too large for rubber mountings.

The 800kg weight will have to be supported on deflection springs so that the weight compresses each spring 10mm. The shape of the cubicle base will dictate where the isolation springs are mounted. For a rectangular base 12 isolators could be used. One placed at each corner and the others equally spaced along each long. From this the spring constant can be calculated …

$$ \displaystyle\large k=\frac{F}{x}=\frac{800kg}{12}\times\frac{9.81m/s^{2}}{0.01m}=65kN/m $$

and the deflection spring arrangement selected from a supplier. In addition to the solution arrived at above there are other considerations.

• The cabinet must be stable for persons working on/in it and the base may need to be redesigned to ensure stability.
•  Supported base frames do not have the floor to provide stiffness and must be structurally sound to provide rigidity and prevent any deflection of equipment.
• For light machines, such as fans, it may be necessary to add mass concrete to the base to provide added weight so that heavier isolators are used to provide stability.
• Where rocking motion exists, such with engines, free standing isolators are unsuitable to prevent motion and constraining isolators are needed to capture the machine. An example is the engine mounts on motor cars that both isolate vibration and prevent the engine coming loose due to vibration.
• Equipment can vibrate in any free direction and if constraining isolators are used it will be necessary to consider natural vibration in other than the principle direction of system components connected together.
• Machines transversing the natural frequency of the isolated equipment (a flexible foundation) may become unstable and the design will need to consider acceptable amplitude limits for the equipment.
• All isolation supports must have the same deflection and it may be necessary to vary the spring rate where equipment masses are located unevenly.