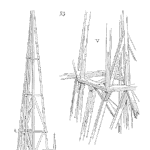
Jezdimir Knezevic of the MIRCE Akademy published a paper with the title above and I have a few comments.
In the article, Jezdimir suggests that the statistical approach to describing the world about us is fundamental flaws and not inherently useful for our use. He compares a mathematical/statistical approach to a scientific approach and finds the stats wanting.
Let’s take a critical look at the topic of this paper and conclusions.
With kind permission of Jezdimir you may find a copy of the paper available for download at the Crimson Publishers site.
Abstract
The paper’s abstract is:
According to Knezevic [1] the purpose of existence of any functionable system is to do function ability work, which is considered to be done when the expected measurable function is performed through time. However, experience teaches us that in-service life of functionable systems is frequently beset by undesirable in-service disturbances resulting from a variety of physical mechanisms (overstress, wear out, natural phenomena and human interventions), some of which result in hazardous consequences to: the users; the natural environment; the general population and businesses. During the last sixty years, Reliability Theory has been used in an effort to predict these occurrences of undesirable in-service disturbances (frequently called failures). However, mathematically and scientifically speaking, the accuracy of these predictions, at best, were only ever valid to the time of the occurrence of the first undesirable in-service event, which is far from satisfactory in the respect of its expected life. Consequently, the main objective of this paper is to raise the question, how reliable are reliability predictions, based on the Reliability Function, in terms of mathematical and physical truth?.
The Gist of the Paper with Comments
The paper starts with a rundown of why the work of reliability minded people matters. I agree that we work to reduce the occurrence of failures and the resulting consequences of those failures.
Then the paper touches on a bit of history. Recounting the use of reliability statistics in the 1950’s along with associated development work since that start. Defining reliability, the probability aspect of the reliability function along with the expansion to the reliability of a system.
What is missing from this history is the accompanying work on the physics of failure approach. The work to fundamentally understand how items fail and the work to model those behaviors. The work in the scientific approach to reliability, unfortunately, takes longer, a larger investment, and still is unable to account for all the variables a particular item may encounter.
The discussion then focuses on the ‘mathematical truth of a reliability function’. It breaks down the necessary consistency of mathematics and the ability of the mathematical functions and equations to just exist within the world of mathematics. Jezdimir then lists about a dozen simplifying assumptions or conditions necessary for the math to work – essentially stated the math of a reliability function has no ability to deal with variability.
During the discussion of the scientific approach to reliability engineering, or the ‘physical truth of reliability function’ he expounds on the messiness of the world in which our items and systems exist. The comparison is summarised by:
Physics, unlike mathematics, is a systematic study of our universe and its rules.
A key fault of the mathematical approach seems to focus on the use of MTBF (and related ill-conceived measures commonly used in reliability work). The use of MTBF in contracts and predictions do not have any basis in mathematics or the physical world when used poorly.
My Review and Comments
In my view of the world, even in a deterministic (scientific) formula, we are using many of the tenets and axioms of good mathematics. As an example, if describing the diffusion of oxygen through a polymer tube wall, we gather the relevant information and arrange the data into a formula for a calculation of the diffusion rate and resulting accumulation over time.
We use math to describe the physical world behavior of diffusion.
Now let’s say the polymer material has some variability in its permeability, or in the wall thickness, or the environment varies its atmospheric pressure. These are real-world occurrences and using statistics (the language of variability) we can expand our deterministic formula to include the actual world variability.
We use the reliability function to describe the real world variability of time to failure, often due to the real-world variability that leads to differences in time to failure for a population of items.
I do agree that if we limit our reliability work to the exponential distribution reliability function, along with the common practice of ignoring variability, we are not doing useful or meaningful work.
There is a middle space ignored in the paper that acknowledges the physics and crude variability of the world along with the power of statistical based mathematics to describe that world. When used well combine science-based models adapted to adequately describe the variability of stresses, materials, uses, etc. we find results that are actually useful.
One last point, I also agree that creating reliability estimates if from any sphere or combination of approaches and is not checked with actual performance is a fruitless exercise. We need learn and continue to learn about the systems we create and the world they exist and along the way provide increasingly useful and practical reliability functions describing the world as it is and as it is expected to perform.
Take some time to read the paper and please comment below. One of my assumptions about creating and publishing a technical paper is to further the discussion and understanding of us all. Join the discussion and let’s continue to learn together.
OK I agree. “Physical truth that is obtained by systematic studies and
analysis of in-service occurrences of undesirable disturbances,
many of which do not feature in the currently used reliability
function. ”
I am working on the “User Manual for ‘Credible Reliability Prediction’.” which uses real reliability instead of mathematical reliability. Meanwhile, pester http://www.asqrd.org to publish “Credible Reliablity Prediction” again: last seen in 2014.
Dear Fred
I read your comments and found then correct.
However, the main point of the paper is that reliability function, however accurate or inaccurate assumptions regarding probability distributions of time to failures are, still addresses the life of an system until FIRST SYSTEM FAILURE.
So, I wished to draw attention of the reliability professionals to start addressing the life of a system after first system failure, or a life of a system with repairable redundant components. As a “picture is worth 1000 words”, please see the attachment.
Looking forward to hearing from you.
With regards
Jezdimir
ps. as i could not insert a picture here, i am sending it to you via email.
Thanks for the note Jezdimir – and here’s the image you sent me via email
I agree that the reliability function is for the time to first failure – and that is appropriate when analyzing something like a bearing, which upon failure is just replaced.
For repairable systems, we are often more interested in availability which as you know incorporates repair times.
For repairable systems, I tend to use a mean cumulative function to describe system performance over time. It helps to know if the maintenance strategy and execution is helping or hurting the system. Still using statistics yet does address issue unique to repairable systems
Cheers,
Fred
I beg to differ: don’t assume dead-forever; you could miss a lot of useful info. Ford 1988 V8-460 cid engine repeated repairs, Firestone tires, M88-A1 tank engine shortages in Kuwait and Iraq, incendiary ignition switches, etc.
Read my job interview story in the “User Manual for Credible Reliability Prediction” linked to https://sites.google.com/site/user-manual-for-credible-reliability-prediction/.
Ships and returns counts (births and deaths in biostatistics) are statistically sufficient to make nonparametric estimates for renewal processes, generalized renewal processes, and some recurrent processes. E.g., Apple computer parts, Abbott Diagnostics Division service parts, automotive aftermarket parts; Firestone tires, Tesla model S battery, charger, and drive units,… At least 3 Oracle-based service dbs list failure times by part name. What if the system contains more than one part of same name? Was second failure, first failure of second part or second failure of first part? EM-algorithm yields nonparametric max. likelihood reliability estimate