First off, switches are not perfect, so this situation includes the reliability of the switch. Switch reliability may be a factor of storage time, probability of actually working when called on to work, or number of switching cycles. Each switch technology may be slightly different. For this equation, you need the reliability or probability of success given the primary unit has failed. Although we are assume the switch reliability is independent of the primary unit reliability and subsequent failure.
Second, in practice we use different equipment or components for the standby redundancy. For example we may use a diesel generator as a back up for grid power. Or use a refurbished pump to back up the main pump. Consider this situation for standby redundancy with equal failure rates (same type and age equipment) and an imperfect ability to detect and turn on the back up unit.
Let’s explore the math to estimate the system reliability given standby redundancy with an example.
Two Power Supply System with One Suppy in Standby
The two supplies have the same expected failure rate, 0.0005 failures per hour, over the duration we expect the system to operate, 730 hours. Only one operates at a time. And, we’re going to include how the second supply is turned on when the first one fails. We’re using an imperfect switch.
Here’s a simple diagram of the situation.
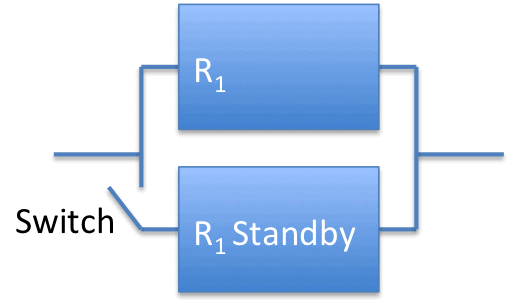
Where R1 is the reliability function of the power supplies. So, what is the reliability expectation of this standby redundancy configuration?
The formula for we can use in this situation is
$$ \large\displaystyle R\left( t \right)={{e}^{-\lambda t}}\left( 1+{{R}_{sw}}\left( t \right)\lambda t \right)$$
This is slightly different then the k-out-of-n formula with a 1-out-of-2 situation as the first unit operates alone while the standby unit is dormant and assumed to have not dormant failure period failures.
Let’s say the switch reliability, $- {{R}_{sw}}\left( t \right) -$, is 95% at 730 hours of system use, in this example.
Adding the values for $- {{R}_{sw}}\left( t \right) -$, t and $- \lambda -$ we find
$$ \large\displaystyle \begin{array}{*{35}{l}}
R\left( 730 \right)={{e}^{-\left( 0.0005 \right)730}}\left( 1+\left( 0.95 \right)\left( 0.0005 \right)730 \right) \\
R\left( 730 \right)={{e}^{-0.365}}\left( 1.347 \right) \\
R\left( 730 \right)=0.935 \\
\end{array}$$
Related:
Standby Redundancy with Equal Failure Rates and Perfect Switching (article)
Parallel Systems (article)
k out of n (article)
I think you should emphasize that this formula is derivated from a binomial distribution and all of the components have constant failure rates.