A discreet distribution useful when counting events within a time period.
It models rates, such as the number of gophers in your garden, paint scratches on your car, or the number of shopping carts that arrive in the 5 minutes before you in line. Essentially it’s the count of something over a time period or defined area.
The Poisson distribution is related to the exponential distribution such that if x is an exponential random variable, the 1/x is a Poisson distributed random variable.
Like an exponential distribution, the chance per interval of time or space provides is equal. For the Poisson distribution, the probability of occurrence is proportional to the length or area of the interval.
In other words, if there is a 1/100 chance of a paint blemish on one square inch of a car door, then there would be a 1/10 chance of a paint blemish over ten square inches of the door.
Probability Density Function, PDF
The PDF for the Poisson distribution is defined by the mean, μ. Thus
$$ \large\displaystyle P\left(x,\mu\right)=f\left(x\right)=\frac{{{e}^{-\mu }}{{\mu }^{x}}}{x!}$$
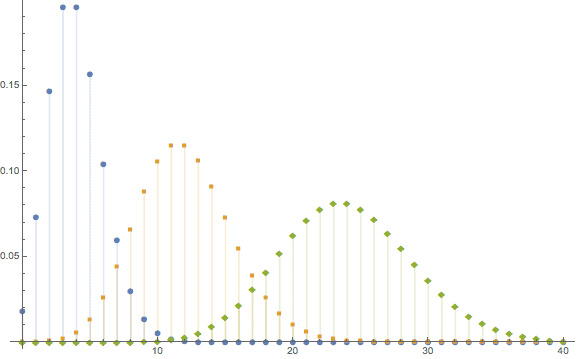
Which determines the probability of exactly x occurrences in an interval having an average of μ occurrence. Setting μ to 4, 12, and 24 and plotting creates
Plotting the PDF it generally appears symmetrical and almost normal distribution shaped. The mean equals the variance for the Poisson distribution though.
$$ \large\displaystyle \mu ={{\sigma }^{2}}$$
Where σ is the standard deviation.
Cumulative Distribution Function, CDF
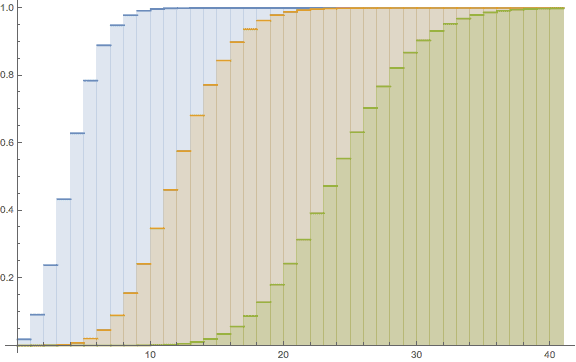
The CDF for the Poisson distribution is defined by the mean, μ, as follows
$$ \large\displaystyle F\left( x \right)=\sum\nolimits_{i=0}^{x}{\frac{{{e}^{-\mu }}{{\mu }^{i}}}{i!}}$$
This is essentially just adding up the probabilities starting with zero up to x of interest. Plotting the same means as above creates
An example is in the previous post Poisson Distribution Calculation.
Related:
The Exponential Distribution (article)
Poisson Distribution Calculation (article)
The Four Functions (article)
Leave a Reply