
Time series forecasts are easy to make and data are available. They’re like driving while looking in the rear-view mirror. A survey listed 31 forecasting software programs: none actuarial [Yurkewicz]. Actuarial failure forecasts are less biased and are more precise than time series failure forecasts, because actuarial failure forecasts use age-specific failure rates. How much better?
The example in this article shows the 5% to 95% time series confidence interval width is 44.78 vs. the nonparametric actuarial Kaplan-Meier actuarial forecast width of 12.63, from grouped failure data, and actuarial forecast width of 15.45, from ships and returns counts.
Contrarians Denigrate Attempts to Improve Forecasts
Tracking products and parts to failure by serial number to obtain lifetime data may incur error. Ralph Evans, former Managing Editor of IEEE Transactions on Reliability, said, “Field-data are largely garbage. I believe they deserve all the negative thinking possible.” Fortunately, accounting methods prevent errors in field data, and accountants get in serious trouble for falsifying data. Therefore, ships and failures or returns avoid suspicion because they are derived from accounting data required by GAAP, revenue, warranty or service costs, or spare parts’ sales.
Conclusions based on sample data incur suspicion. Tversky and Kahneman said, “It’s human nature to disbelieve statistically significant conclusions from a sample that is a small fraction of the population.” Fortunately, accounting data is population, not sample data, so time series and actuarial forecasts computed from ships and returns have no sample uncertainty.
James Krupp discusses forecasts for the automotive aftermarket. He writes, “The data required to provide an expected replacement profile are not automatically available at this time; thus, the expansion of this theory [actuarial forecasts] into full practical applications will require future efforts in developing reliable bases of information.” By replacement profile,Krupp meant actuarial rates. I.e., actuarial forecasts can’t be made without actuarial rates and actuarial rates were not available. Krupp kvetched when I quoted him in an SAE publication on estimating and using actuarial forecasts for the automotive aftermarket.
“To predict demand one would have to keep a tally of how many parts are in service, how many hours of operation each part has endured, and how much wear occurred during those hours. Furthermore, these data are worthless without a reliability model relating part use to the probability of replacement. Most service parts distributors do not have the expertise to make a reliability model for each part type nor access to customer data about part usage” [www.smartcorp.com]. Triad Computer Systems did [US Patent number 5,765,143].
Alternatives?
Some authors describe functional data analysis to derive mortality forecasts. They include the effect of the birth year by regarding log-hazard functions, derived from observed cohort lifetables [same as input to Kaplan-Meier estimator], as random functions. A functional model for the analysis of these cohort log hazard functions, extending functional principal component approaches by introducing time-varying eigenfunctions [Chiou and Müller, Hyndman and Ullah].
Others use multivariate times series to incorporate periodic cohort sizes in addition to observed periodic failure counts. Most use multivariate time series to extrapolate each component’s time series. This seems popular among AI and machine learning users. Does anyone use multivariate times series analysis to improve the forecast of one component time series such as failures?
Actuarial Forecasts Account for the Forces of Mortality
Actuarial forecasts are ∑a(t-s)*n(s), s=0,1,2,…,t, where n(s) is the installed base of age s and a(t-s) is the failure rate conditional on survival to age t-s. Actuarial forecasts look ahead by accounting for the forces of mortality in actuarial failure or demand rates. For example: process defects cause infant mortality, inappropriate sales cause NTFs (no trouble found), WEAP (warranty expiration anticipation phenomenon) causes failures around warranty, preventive maintenance discovers or causes failures around PM times, wearout causes failures. GAAP requires sufficient data to make actuarial forecasts for products and service parts. Why not make actuarial forecasts?
Actuarial forecasters track parts by serial number to obtain ages at failures and estimate actuarial rates. Tracking parts by serial number is not necessary! It requires 1000 times as much data storage as ships and returns counts, and it incurs at least 1000 times as many errors.
Life insurance and actuarial statistics are so pervasive that they hardly need mention. (If you’re over 72 years old and have an IRA, your required minimum distribution is based on your actuarial death rate.) The Air Force Air Material Command uses the “actuarial method” developed by Rand Corporation 60 years ago for engines and expensive subassemblies tracked by name and serial number from birth to death [AFLCM 66-7 and AFM 400-1].
“Actuaries fix insurance prices not to match past costs but to balance a stream of future expected costs. Reserves reflect expectations about the insufficiency of future income to balance future claim payments” [Miller and Hickman].
Assumptions that are no longer valid:
- Need to track units by serial number or name from birth to death
- Covariance of actuarial rate estimates is zero
- Demand distribution is Poisson [AFLCM 66-7 and AFM 400-1, Triad Computer Systems US Patent 5765143], negative binomial [John Muckstadt, Robin Roundy US Patent 5287267],
- Can’t estimate actuarial rates from ships and returns counts [Krupp, Maisel, SmartCorp].
Compare Confidence Limits on Time Series vs. Actuarial Demand Forecasts?
The Kaplan-Meier nonparametric reliability estimator from censored, lifetime failure counts grouped by cohort provides actuarial rate estimates. Lifetime data is not required to estimate actuarial rates. Generally accepted accounting principles require ships and returns counts, which are statistically sufficient for estimating reliability and age-specific actuarial rates, without model assumptions [George].
Confidence limits on demand forecasts are used to set inventory stock levels, because the lower confidence limit (LCL) corresponds to the probability of stockout or back-order, and the upper confidence limit (UCL) helps determine order quantities. Confidence limits on time series forecasts have been available, since before Williams and Goodman’s 1977 simple idea. [Pedants complain that confidence limits on forecasts are “prediction limits”.]
Table 1 shows part of the input data to making the Kaplan-Meier (K-M) reliability estimate. The ships column and the bottom row sums (returns) are statistically sufficient to make nonparametric likelihood reliability estimates [George]. Figure 1 shows the actuarial rate estimates derived from the reliability estimates.
Table 1. Periodic ships (cohort sizes) and grouped failure counts (Nevada table).
| Period | Ships | 1 | 2 | 3 | Etc. | 18 |
| 1 | 47 | 1 | 3 | 7 | 0 | |
| 2 | 41 | 4 | 3 | 0 | ||
| 3 | 45 | 2 | 0 | |||
| Etc. | ||||||
| 18 | 42 | |||||
| Sums | 1 | 7 | 12 | 37 |
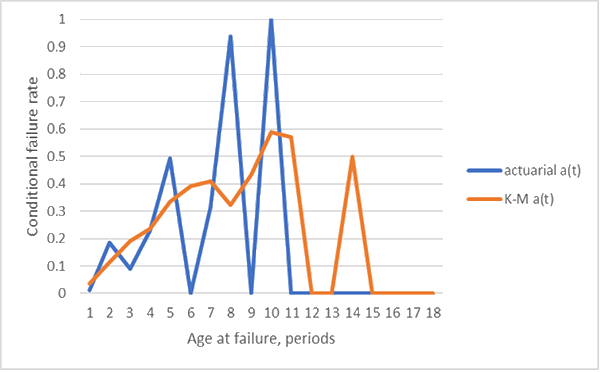
Table 2 contains observed returns (failures) in periods 1-18 and alternative forecasts for period 19. The Excel FORECAST.ETS() time-series forecast for period 19 is in column 2. Actuarial hindcasts for period 1-18 and forecast for period 19 are in columns 3 (Kaplan-Meier actuarial rates) and column 4 (nonparametric maximum likelihood actuarial rates).
Excel’s FORECAST.ETS.CONFINT function fails! The FORECAST.ETS.CONFINT 5% and 95% confidence limits in column 2 are 0.67 and 21.06; they don’t even include the period 19 FORECAST.ETS of 38.66! So I constructed confidence limits based on (assumed normal) errors in alternative forecasts. [Williams and Goodman] To replace FORECAST.ETS.CONFINT, column 5 makes FORECAST.ETS hindcasts for periods 1-18. The 5% and 95% confidence limits for the forecasts use the means and standard deviations of the errors (observed returns – hindcasts). The K-M forecast (35.29) confidence limits (28.97, 41.60) are slightly tighter than those from the npmle forecast (34.51) from ships and returns “npmle S&R”, (26.79, 42.24), because there is more information in grouped failure counts by cohort than in period sums of returns counts. The forecast from period FORECAST.ETS hindcast is still 38.66 but the normal 5% and 95% confidence limits are large, (16.27, 61.05).
Table 2. Compare actuarial forecasts (K-M and npmle S&R) vs. time series (FORECAST.ETS), their confidence limits and widths.
| Period | Returns | K-M | npmle S&R | FORECAST.ETS |
| 1 | 1 | 1.65 | 0.53 | 8.79 |
| 2 | 7 | 6.65 | 9.02 | 10.45 |
| 3 | 12 | 13.96 | 11.21 | 12.11 |
| Etc. | ||||
| 18 | 37 | 35.20 | 28.84 | 37.00 |
| 19 forecasts | 38.66 | 35.29 | 34.51 | 38.66 |
| 5% LCL | 0.67 | 28.97 | 26.79 | 16.27 |
| 95% UCL | 21.06 | 41.60 | 42.24 | 61.05 |
| Width | NA | 12.63 | 15.45 | 44.78 |
Triad Computer Systems, CCI-Triad, Activant, and Epicor
Founded in 1971, Triad computerized auto aftermarket parts stores. In 1995, Triad’s New Products Manager (econometrician) tried regression to make auto parts’ demand forecasts using vehicle registrations and part sales in nearby stores, Sales(part, t) =Sb(s)*n(s), s=1,2,…,t where b(s) are regression coefficients and n(s) is registered vehicle count in the store neighborhood that used the part. Regression failed because of autocorrelation. (No pun intended.)
I pointed out that the regression model was an actuarial forecast where the regression coefficients b(s) were actuarial rates. We computed actuarial rates from parts’ counts (computed from vehicle counts and Triad catalogs that told which parts and how many go into which vehicles), and periodic store sales by part number [U.S. patent number 5,765,143]. We made parts’ demand forecasts and recommended stock levels.
Triad made so much money off actuarial forecasts and stock recommendations that it was bought in a leveraged buyout by a competitor, CCI, in year 2000. CCI said do as much as you can for as little $$$ as possible. So they laid off the New Products Manager and me. Later, company principals took over and ran it under the name “Activant” in 2003. That was merged with Epicor Software in 2011. KKR bought Epicor in 2020 so I sold my KKR stock. KKR sold Epicor to Clayton, Dubilier, and Rice, and KKR stock rose 1.9%.
A member of the New Products group took over and contracted www.smartcorp.com to make time series forecasts of auto parts’ demands, because he didn’t understand actuarial and reliability statistics. Evidently unsatisfied with the SmartCorp time series forecasts, the New Products group manager (“Senior Director and Business Leader, Industrial Analytics”) contracted AI company www.Predii.com to make auto parts’ demand forecasts and provide service recommendations. He was finally fired for promising and not delivering. I wonder how Epicor time series and AI forecasts and stock recommendations are doing now?
References
AFLCM 66-17, “Quantitative Analyses, Forecasting, and Integrative Management Techniques for Maintenance Planning and Control,” U.S. Air Force Logistics Command, Wright-Patterson AFB, Ohio, March 27, 1970, revised June 20, 1973
AFM 400-1, “Logistics, Selective Management of Propulsion Units, Policy and Guidance,” U.S. Air Force, June 21, 1976
Jeng-Min Chiou and Hans-Georg Müller, “Modeling Hazard Rates as Functional Data for the Analysis of Cohort Lifetables and Mortality Forecasting,” October 2008
L. L. George, “Actuarial Forecasts Without Life Data,” International Symposium on Forecasting, Washington, D.C., June 1999
L. L. George, “Actuarial Forecasts for the Automotive Aftermarket,” SAE-01-1538, 2004
Patric Oscarsson and Örjan Hallberg, “ERIVIEW 2000 – A Tool for the Analysis of Field Statistics,” Ericsson Telecom AB, http://home.swipnet.se/~w-78067/ERI2000.PDF, 2000
Carl M. Harris and Edward Rattner, “Estimating and projecting regional HIV/AIDS cases and costs, 1990-2000: A case study,” Interfaces, Vol. 27, No. 5, pp. 38-53, 1997
Rob J Hyndman and Md Shahid Ullah, “Robust forecasting of mortality and fertility rates: a functional data approach,” Elsevier, 2006
Krupp, J. A. G., “Forecasting for the Automotive Aftermarket,” The J. of Bus. Forecasting, pp. 8-12, Winter, 1993-94
William H. Maisel, MD, MPH, ”Pacemaker and ICD Generator Reliability, Meta-analysis of Device Registries,” JAMA, Vol. 295, No. 16, pp. 1929-1934, April 26, 2006
Robert B. Miller and James C. Hickman, “Time Series Analysis and Forecasting,” Transactions of Society of Actuaries,Vol. 25 Pt. 1, No. 73, 1973
SmartCorp, “What You Need to Know About Forecasting and Planning Service Parts” White Paper, www.smartcorp.com,
William (Bill) H. Williams and M. L. Goodman, “A Simple Method for the Construction of Empirical Confidence Limits for Economic Forecasts,” William (Bill) H. Williams and M. L. Goodman, J. Amer. Statist. Assn., Vol. 66, no. 336, pp. 752-754, Dec. 1971
Yurkiewicz, Jack, “Forecasting Software Survey,” OR/MS Today, Vol. 33, No. 4, pp. 40-49, Aug 2006
 Ask a question or send along a comment.
Please login to view and use the contact form.
Ask a question or send along a comment.
Please login to view and use the contact form.
Leave a Reply