
Vibration in equipment is the result of unbalanced forces.
Out-of-balance is corrected by adding or removing material so that when the equipment is operating the unbalance is controlled to an acceptable level.
Keywords: spring stiffness, damping, center of rotation, center of mass, natural frequency, isolation mount, counterbalance, out-of-phase.
The transference of unbalanced forces through equipment into neighboring structures causing them to shake is vibration.
The motion of a body is limited by what connects it to a machine and the walls in which it moves. Every time there is a change of direction unbalanced forces produce a shock.
This shock travels throughout the machine and is transmitted to all connected items.
Mostly a spring is used to isolate vibration movement or a damper is used to absorb the movement. A full explanation of vibration control requires calculus and is beyond the scope of this article.
The spring-mass-damper system sketch below is a simplified representation of a vibration control system.
Spring force and damper pressure control the mass’ movement.
The damper piston moves and so absorbs the vibration. Whereas the spring flexes and isolates the movement from its attachment.
The rate of vibration is called the frequency.
It is measured in cycles per second and has the units Hertz. A four-pole electric motor rotates at about 1500 RPM. This is 25 cycles per second or 25 Hertz.
Vibration caused by an external applied force is known as a forced vibration because the mass oscillates at the frequency of the external force.
An example is the shake produced by the moving pistons and crankshaft in a car engine.
The equation for the natural frequency of an undamped spring-mass system moving in one direction is
$$ {{f}_{n}}=\frac{1}{2}\pi \sqrt{\left( \frac{K}{M} \right)}$$
where K is the spring stiffness and M the mass.
This equation lets us find the resonance frequency for a mass–spring system.
Such a system can be represented in the drawing above by removing the damper.
Wild gyrations develop when the forced frequency nears the system natural frequency. Every system has a natural frequency and will shake to destruction if it is forced to move at that rate.
This phenomenon is known as resonance.
An example would be the shattered wine glass caused by an opera singer’s voice or vibrations in long, thin shafts that start and then stop as the shaft speed goes through its natural frequency speed.
The four methods of vibration control are listed below.
- Reduce or eliminate the exciting force by balance or removal.
- Use sufficient damping to limit amplitude.
- Isolate the vibration source from the surrounds by using spring mounts of appropriate stiffness.
- Introduce a counterbalancing force opposite in phase to the exciting force.
Most importantly every moving mass must be balanced about its center of rotation.
The topic of rotary machine balancing was introduced in the article “When Spinning Equipment is Unbalanced“. The article indicated that rotating masses must be balanced to an acceptable standard.
Out–of-balance rotors cause vibration because the center of mass of the rotor is eccentric (not running true) to its center of rotation.
The spinning off-center mass is continually being flung outward. The machine’s bearings hold the mass in place and react against the developed forces.
Vibration results as first the mass is on one side of the bearings and then it is on the other.
Balancing aims to distribute the mass evenly about the running center.
The drawing below shows eccentricity between the center of mass and the center of rotation.
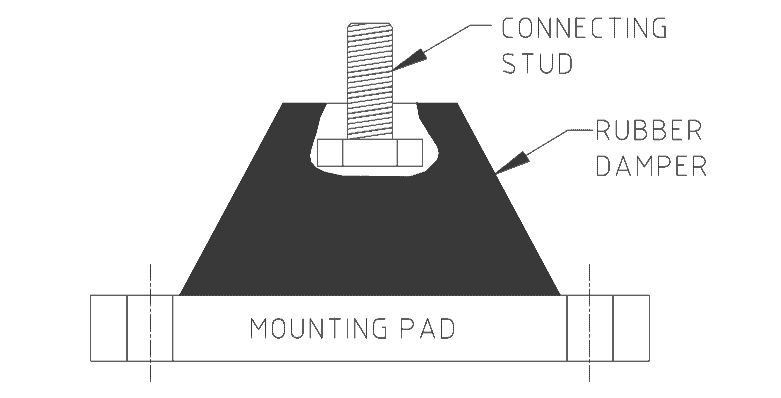
Materials such as rubber dampen shaking.
The rubber flexes and absorbs the movement within itself.
The sketch below is a simple rubber vibration damper. Because rubber cannot compress much to accommodate movement, rubber dampers are normally used for low amplitude, high-frequency vibration where noise transference is a problem.
Shock absorbers are used for large amplitude, low-frequency situations where springs alone would produce bouncing. An example is in car suspensions.
The natural frequency can be moved away from the forcing frequency by changing the weight of the system.
Making the frame of a vibrating machine heavier will lower the assembly’s natural frequency.
Concrete added to the base frames of lightweight fans reduce vibration by lowering the natural frequency and moving it away from the forcing frequency produced by the rotating blades.
A vibrating mass can also be isolated from its surroundings by springs.
The springs deflect under the shaking body. Installing isolation springs make the spring’s natural frequency the governing frequency for vibration transfer. Altering the spring stiffness allows us to select the desired amount of isolation.
Spring stiffness controls the amount of vibration transferred to the attachment.
Too stiff will transmit vibration, while insufficient stiffness will cause bounce.
The correct spring stiffness can be found using charts available from specialist vibration control companies. The isolation springs must not have a natural frequency near the forcing frequency of the isolated equipment.
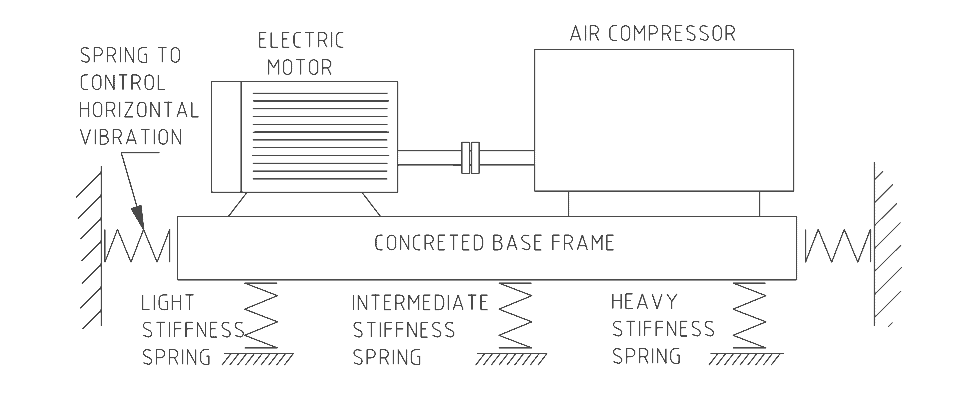
In such a case the system would start to resonate and jump about. The sketch below shows an air compressor supported on springs.
Stiffer springs are at the heavier end of the machine to both keep the machine level and to prevent resonance developing as the mass increases.
The drawing also indicates that vibration is usually in more than one direction.
An out-of-phase mass is a method not often used to control vibration.
It is possible to use a weight with an opposite vibration pattern to negate the out-of-balance forces.
This method has been used in motor car engines where a shaft with an eccentric mass is spun in the opposite direction to the crankshaft.
Mike Sondalini – Maintenance Engineer
If you found this interesting, you may like the ebook Process Control Essentials.
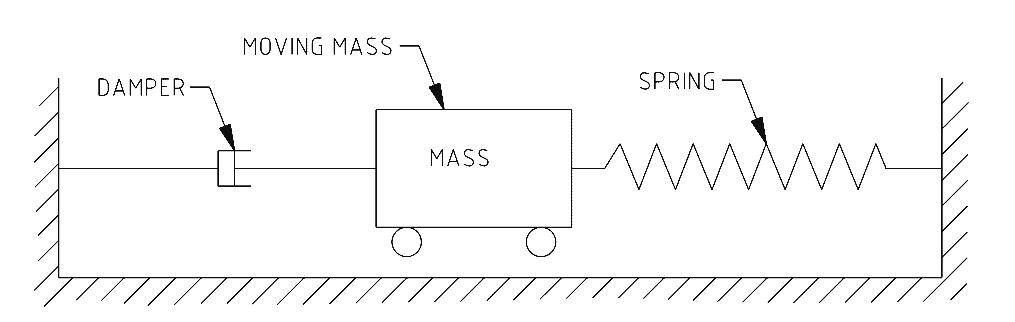

 Ask a question or send along a comment.
Please login to view and use the contact form.
Ask a question or send along a comment.
Please login to view and use the contact form.
Thanks for your explanation on how vibration is controlled. It is the most detailed article I have seen. I just have a question about the springs used to control vibration. How long does it take for spring stiffness to be compromised in a vibrating motor? Is it a commonly replaced part?
A four-pole electric motor rotates at about 1500 RPM. This is 25 cycles per second or 25 Hertz.
Is this correct?
By equation N (R.P.M) equals to 120 f (Hz)/P ( no. of poles).
Calculating gets 50 Hz.