
Each piece of gear used in rock climbing has the potential to be the weakest link. Often, based on accident reports, it the human decisions or lack of focus that is the most difficult to improve.
Ropes, anchors, harness, and carabiners and another equipment all have to work in the event of a fall. The design of each piece of equipment is to meet and hopefully exceed any possible load. And, to maintain the needed strength over years of harsh outdoor use.
Most products today would benefit from such a design approach. The approach of making each part as strong or stronger than any other element in the system and much stronger than expected loads. We’ll talk more about stress/strength and derating in another post, today, I want to focus on the series system model and the associated simple reliability block diagram. This is similar to reliability apportionment discussed in another post, yet rather than a top-down goal setting process, we are gathering information at each element in the model and calculating the system reliability.
The product of the reliability of each element in a series model results in the system reliability. Of course, there are a few assumptions. First, that any element can cause the system to fail. While this is not always true for every component within a system, in most products is close enough to be useful.
Second, each element within the system experiences the applied stress, bears the load, and wears independently from the other elements. We’re assuming that the increasing resistance and heat generated by one part does not significantly change the probability of failure over time of the other elements. This is often not true, strictly, yet the added burden of modeling all the interactions would render the model too difficult to build, maintain and use. If there are significant interactions within the system, consider a more complex model.
While many books and references at this point in the discussion use an example with exponential distributions for each element, let’s ponder a moment that few components have a life distribution that enjoys a constant failure rate. Remember that using exponential distributions (MTBF, FIT, or similar single parameter descriptions of the life distribution) is a very simplifying method to do series system reliability calculations –
if restricted to using mechanical adding machines!
With modern calculators and computers, it is as easy to sum a set of number as it is to determine the product. We can use the reliability functions directly by simply multiplying the element reliability functions together at any point in time, t, of interest.
So, since you will probably see a problem with the assumption of the exponential distribution, here is the reliability function
And, making the assumption that all the elements of the system are adequately (choke, cough) described by the exponential distribution, we can simply sum the element failure rates.
This works, it’s easy, and most often a very poor estimate of the system reliability. You most likely will encounter this on the CRE and most likely at work, too.
So, the same series model permits us to consider each elements failure mechanisms or model of the time to failure as appropriate and without limiting assumptions constraining the life modeling to a one parameter distribution. We can use Weibull for one element, Lognormal for another, and Exponential as needed and appropriate for another.
(for some reason the enclosing parenthesis and mu are not showing for the lognormal reliability function)
The strength of the series system model is in its simplicity. Not in its ability to be simple. Describing the reliability function accurately for each element provide a clearer model of the reliability performance over time, thus permitting the design team to address the weakest link appropriately.
Related:
Reliability Block Diagrams Overview and Value (article)
Reliability Apportionment (article)
Parallel Systems (article)
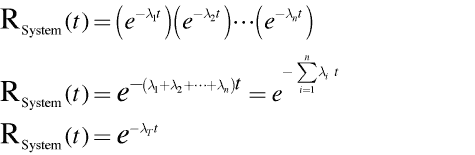

 Ask a question or send along a comment.
Please login to view and use the contact form.
Ask a question or send along a comment.
Please login to view and use the contact form.
Leave a Reply