In manufacturing and quality assurance, we rarely have the time—or budget—to inspect every single part in a batch. That’s where acceptance sampling comes in. It’s a statistical tool that helps us decide whether to accept or reject a lot of material based on a random sample. But more than just a shortcut, acceptance sampling is a structured decision-making process that balances quality expectations with efficiency and risk.
The Big Idea Behind Acceptance Sampling
Acceptance sampling plans are built around the idea of acceptable quality level, or AQL. The AQL defines the worst-case quality level that is still considered acceptable for a particular process or customer. It’s the maximum percent defective that can exist in a lot for it to be considered satisfactory.
For example, an AQL of 0.65% means that, on average, up to 0.65% of the units in a lot could be defective—and that would still be considered acceptable. Lower AQLs represent tighter quality expectations and a lower tolerance for risk.
A sampling plan includes three main elements:
- Lot size (how many parts are in the batch),
- Sample size (how many parts you’ll inspect), and
- Acceptance number (the maximum number of defects you can find before rejecting the lot).
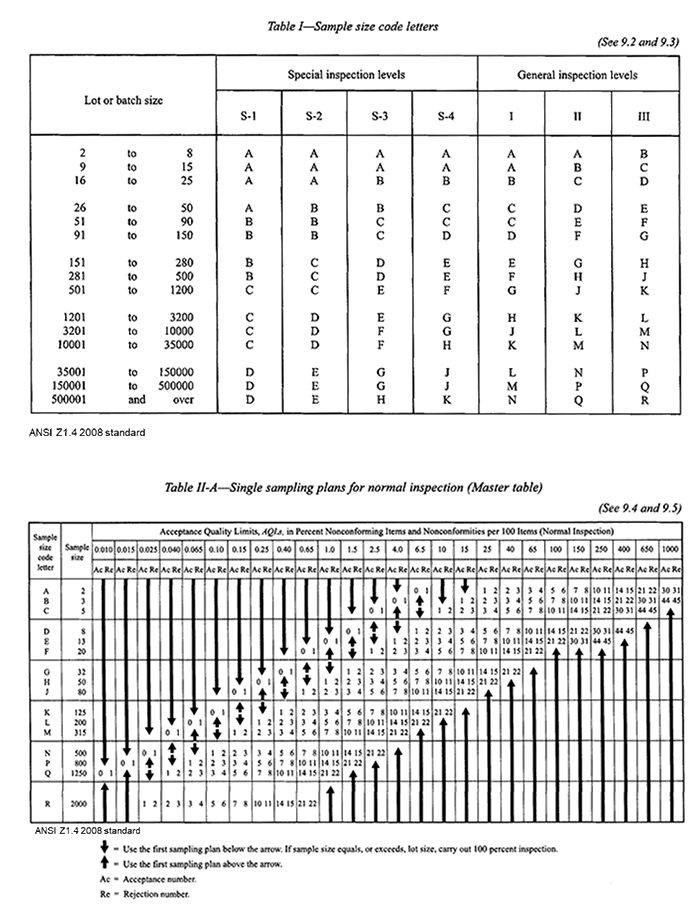
These are linked. If you tighten the AQL, you’ll usually need a larger sample size and fewer allowable defects. All of these parameters are laid out in standardized tables, such as those found in ANSI/ASQ Z1.4-2008.
An Example Using Z1.4
Let’s say you’re working with a lot of 1,000 parts. According to the ANSI Z1.4 tables, you’d locate the appropriate line for your lot size (say, between 501 and 1,200). You’d then choose an inspection level—Level II is a common starting point. That leads you to a code letter, say J, which corresponds to a sample size of 80.
Now, let’s say you’re using a C=0 sampling plan (meaning you reject the lot if you find even one defect). That plan corresponds to an AQL of 0.15% for this sample size. In other words, you’re saying: “I’m only willing to accept this lot if zero defects are found in a sample of 80.” That’s a very strict quality requirement.
If instead you’re working with a more forgiving AQL—say, 1.5%—the tables might allow you to accept the lot if there are up to three defects in the sample, and reject it if there are four or more.
Sampling Always Involves Risk
Every sampling plan involves two kinds of statistical risk:
- Producer’s Risk (Alpha Risk): This is the chance that you’ll reject a good lot—one that actually meets the quality level you’re aiming for. Maybe the defects are spread out evenly in the batch, but you happened to find several in your random sample. That’s frustrating for the producer who knows their batch was good.
- Consumer’s Risk (Beta Risk): This is the chance that you’ll accept a bad lot—one that exceeds your AQL. This happens when your sample misses the defects that are actually in the batch. That’s a risk for the customer, who might end up receiving material that doesn’t meet their quality expectations.
Both of these risks are part of the trade-off in acceptance sampling. You’re not guaranteeing perfection—you’re managing risk using statistics.
It’s Not Just Math—It’s a Decision-Making Tool
One thing that’s important to remember: acceptance sampling is not just a statistical exercise. It’s used to make real decisions. Based on the sample, will you approve the lot for shipment? Will you hold it for additional inspection? Will you initiate a corrective action?
In that sense, acceptance sampling is part of a broader quality strategy. It helps you focus your resources, maintain reasonable inspection costs, and meet your customers’ expectations—all while acknowledging that every decision has some uncertainty.
Want to Dig Deeper?
If you’re curious, ANSI/ASQ Z1.4-2008 is the standard that defines single, double, and multiple sampling plans. It’s where all those tables and rules come from. There are also variable sampling plans described in ANSI Z1.9, but they’re less commonly used in industry because of their complexity.
And no matter what kind of plan you use, random sampling is key. The statistical validity of acceptance sampling depends on pulling a sample that fairly represents the entire lot.
Whether you’re a quality technician pulling samples or an engineer setting quality standards, understanding how acceptance sampling works helps you make better, more informed decisions. It’s not about perfection—it’s about managing quality with confidence.
Author’s Biography
Ray Harkins is the General Manager of Lexington Technologies in Lexington, North Carolina. He earned his Master of Science from Rochester Institute of Technology and his Master of Business Administration from Youngstown State University. He also teaches manufacturing and business-related skills such as Quality Engineering Statistics, Reliability Engineering Statistics, Failure Modes and Effects Analysis (FMEA), and Root Cause Analysis and the 8D Corrective Action Process through the online learning platform, Udemy.
Leave a Reply