Control charts help us monitor and stabilize a process. A little graphics along with statistics provides a tool to identify when something has changed. Some changes are abrupt and obvious, other a little more subtle, yet the out of control signals each have approximately the same chance of alerting us to a change.
A little graphics along with statistics provides a tool to identify when something has changed. Some changes are abrupt and obvious, other a little more subtle, yet the out of control signals each have approximately the same chance of alerting us to a change.
What is the chance the next sample taken and plotted on a control chart will signal a change, when in fact the process has changed? We may be interested specifically if running an experiment (changing parameters, installing new equipment, trying a new material, etc.). How much change will provide an alert right away? Or what is the chance of a signal with a modest shift in the mean?
This problem takes a bit of mental gymnastics along with a solid understanding of control chart construction to solve. Let’s take a look at one way to solve this type of problem.
Currently a Stable process
Let’s say you have been using an X̄ and R control chart on your process for some time. It is stable. The center line is at 185.5 grams and the R̄ center line is at 12.3 grams. We use 5 boxes for each sample, thus n = 5.
You have noticed that the average weight of the final product, 198.5 grams, is just a little below the center of the specification, 200 grams. Thus you would like to change the process to increase the resulting weight by an average of 1.5 grams while maintaining the same variation and stability.
Next Monday you plan to change the process by adding a new material to the mix. You expect it to increase the average weight right away. You would also like to know if the existing control charts will detect the change. The ongoing process distribution is reflected by the blue normal curve imposed on the existing part of the chart.
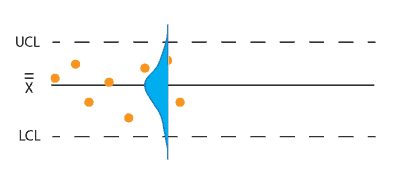
We are deliberately shifting the process up by 1.5 grams, thus shifting the normal curve up by 1.5 represented by the red curve below. What is the chance of having an out of control signal with the first sample?
Determine the control limits
In our notes we have the center line values the two charts, and didn’t note the upper control limit (UCL) value. Rather than track down that value from the chart or the supporting notes, we have enough information to calculate the UCL directly.
We need the UCL value as we want to estimate the change in the amount of the distribution that now exceeds the UCL. For the previous stable process, the UCL marked the point where we would expect an approximately 0.15% chance that a point would fall above the UCL. With the process shift, the probability is now larger.
To estimate the UCL given the X-bar and R charge center lines, recall that the formula for the UCL is
$$ \large\displaystyle UC{{L}_{{\bar{X}}}}=\bar{\bar{X}}+{{A}_{2}}\bar{R}$$
A2 is the tabulated factor to convert the average range to the UCL on the X-bar chart. With 5 measurements per sample, n = 5, and A2 = 0.58. This becomes
$$ \large\displaystyle UC{{L}_{{\bar{X}}}}=198.5+0.58\left( 12.3 \right)=205.6$$
The distance between the center line the UCL is 3 standard deviations of the averages (not the individual readings) when using 5 readings per sample. If we determine this standard error about the mean value, we can use that to determine the number z-value for the shifted process average to the old UCL.
Subtracting out the grand average from the UCL we find 205.6 – 198.5 = 7.1. And since
$$ \large\displaystyle \begin{array}{l}3{{s}_{{\bar{X}}}}={{A}_{2}}\bar{R}=7.1\\{{s}_{{\bar{X}}}}=2.37\end{array}$$
To find the z-value we want to find the distance between the new (expected) center line, 200 grams, and the former UCL, 205.6 grams divided by the sx-bar.
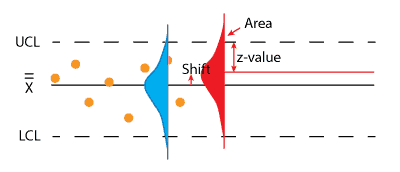The shift up of the red curve shortens the distance between the distribution center and the UCL, thus increasing the area under the curve beyond the UCL line. The z-value is found with
$$ \large\displaystyle z=\frac{UCL-{{{\bar{\bar{X}}}}_{new}}}{{{s}_{{\bar{X}}}}}=\frac{205.6-200}{2.37}=2.36$$
Using the standard normal table in the appendix of your favorite stats book you will find the upper tail beyond a z value of 2.36 is 0.0091. Thus the probability of the first sample resulting in an out of control signal is 0.0091 or 0.91%.
This is not likely to occur as it is approximately a 1 in 100 chance, yet over time the sampling will produce enough points to detect the shift, plus to calculate the new process average and compare to the previous process values with a hypothesis test which is the subject of another article.
Related:
Variables Control Chart Background (article)
When are we out of control (article)
Special and Common Causes of Process Variation (article)
Leave a Reply