
What readers will learn in this article.
- Centrifugal pumps can be moved to a new service.
- The impeller size, impeller speed, and motor power need to match the new service.
- That Similarity Law formula is used in calculating the new impeller size, speed, and motor power.
- Introduction to centrifugal pump curves and their use.
When there is a need to determine a new service duty for a centrifugal pump, and no performance curves are available, the recommended method is to use the Similarity Laws. These laws are derived by the use of dimensional analysis in which selected variables affecting performance are grouped in such a way that permit prediction of scaling effects when the variables are altered. The laws are:
$$ \large\displaystyle\frac{{{Q}_{1}}}{{{Q}_{2}}}=\frac{{{N}_{1}}}{{{N}_{2}}}\frac{D_{1}^{3}}{D_{2}^{3}}\qquad\frac{{{H}_{1}}}{{{H}_{2}}}=\frac{N_{1}^{2}}{N_{2}^{2}}\frac{D_{1}^{2}}{D_{2}^{2}}\qquad\frac{{{P}_{1}}}{{{P}_{2}}}=\frac{{{\rho }_{1}}N_{1}^{3}}{{{\rho }_{2}}N_{2}^{3}}\frac{D_{1}^{5}}{D_{2}^{5}}$$
Where: Q is discharge flow in l/sec.
D is impeller diameter in mm.
ρ is density in kg/m3.
N is impeller speed in rpm.
H is discharge head in meters.
Subscripts 1 and 2 represent initial and final conditions respectively.
If in the equations above, the impeller diameter is held constant and the density is unchanged, the formulas reduce to the well-known Affinity Laws.
$$ \large\displaystyle\frac{{{Q}_{1}}}{{{Q}_{2}}}=\frac{{{N}_{1}}}{{{N}_{2}}}\qquad\frac{{{H}_{1}}}{{{H}_{2}}}=\frac{N_{1}^{2}}{N_{2}^{2}}\qquad\frac{{{P}_{1}}}{{{P}_{2}}}=\frac{N_{1}^{3}}{N_{2}^{3}}$$
The users of these laws put a lot of faith in their ability to predict the required changes to a pump to achieve a new duty. Once the pump is altered it is costly to reverse. But how accurate are these formulas? To determine this, they are used to establish a new duty point for a centrifugal pump pumping water and the result compared to the published pump curves. The difference between the curves and the laws is then observable.
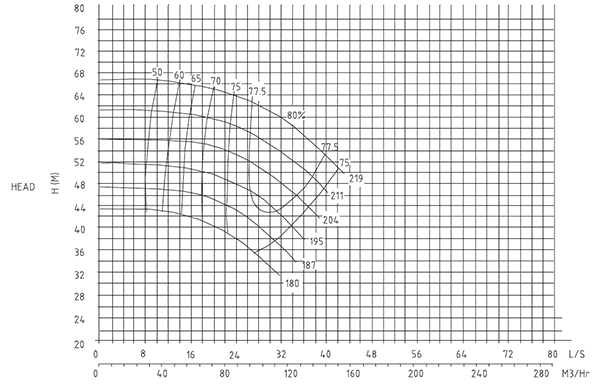
The calculations are for a commonly encountered situation where a pump’s delivery head is to be reduced. In this case, the impeller will require machining to a smaller diameter. The pump has an existing duty of 24 l/sec at the 64m head with an impeller of diameter 219 mm. If the impeller diameter is reduced to 195 mm what is the new duty point calculated by the Similarity Laws? The applicable curves for the 219 mm and 195 mm impellers are shown in Figure 1.
Changing impeller size affects both the pump discharge head and the flow. This requires the use of the Similarity Laws to calculate both the new head and the new flow.
| START POINT | CALCULATED POINT | CURVE POINT | PERCENT DIFF. |
| Q1 = 24 l/sec H1 = 64 m D1 = 219 mm N1 = 2900 rpm | Q2 = 16.9/sec H2 = 50.7 m D2 = 195 mm N2 = 2900 rpm | Q2 = 17/sec H2 = 50.7 m D2 = 195 mm N2 = 2900 rpm | negligible negligible |
If instead the impeller diameter is reduced to 180 mm we get the following results.
| START POINT | CALCULATED POINT | CURVE POINT | PERCENT DIFF. |
| Q1 = 24 l/sec H1 = 64 m D1 = 219 mm N1 = 2900 rpm | Q2 = 13.3 l/sec H2 = 43.2 m D2 = 165 mm N2 = 2900 rpm | Q2 = 13.3 l/sec H2 = 42.8 m D2 = 165 mm N2 = 2900 rpm | negligible 1 |
From the results of the calculations, it is clear that for this manufacturer’s pump the error in using the Similarity Laws is minor though it becomes larger the further the required duty point is from the existing duty point. These results provide some confidence in the use of the formulas. However, when the same method was used for another manufacturer’s pumps a discrepancy between the similarity laws and the pump curves of up to 7 percent was noted. The results are not always exact.
In situations where it is necessary to machine the impeller diameter down it is sensible to leave the impeller larger than calculated and reinstall it. Then establish the intermediate duty point and again calculate what impeller reduction is needed to attain the final required duty point.
For the alternate situation where a higher delivered head or flow is required, the Similarity Laws can be used to estimate the new faster impeller speed or to size a new larger impeller. When increasing the speed or the diameter of an impeller a higher head, flow and power draw result. The appropriate Similarity Law will provide a means to closely estimate the extent of the resulting change.
Mike Sondalini – Maintenance Engineer
DISCLAIMER: Because the authors, publisher, and resellers do not know the context in which the information presented in the articles is to be used, they accept no responsibility for the consequences of using the information.
We (Accendo Reliability) published this article with the kind permission of Feed Forward Publishing, a subsidiary of BIN95.com
Web: trade-school.education
E-mail: info@trade-school.education
If you found this interesting you may like the ebook Pumping Basics.
It looks like that use of similarity law is very useful in calculating accurate values of the impeller speed or size (diameter) according to required head or flow. A tiny computer program should rather be used to calculate these values for the purpose of accuracy and error free calculations.
Khan
Fincio.com
Hi Khan, agree a program or app would be a useful too. Knowing how the app comes up with the value is also worth understanding. Do you have a recommendation for an application that can do these calculations? cheers, Fred