

As I rode, I thought, how could I use reliability statistics to optimize a solar-tube production line? Then I noticed a brass glint in the scrub brush. It didn’t look like trash, so I stopped and found an old brass oil lamp like Aladdin’s. Naturally, I rubbed it. There was a flash and a puff of smoke, and out popped the genie who said, “Yes master, by the powers vested in me, I grant you three wishes.”

I told the genie of my line optimization problem and asked what the genie knew about solar-tube production lines.
He replied, “I know about solar cells, but what’s a solar tube?”
I told the genie that solar tubes are glass, cylindrical solar cells that collect sunlight from any angle and that I wanted to use reliability statistics to help optimize design and operation of a solar-tube production line.
The genie said, “Production lines are not a problem for genies’ cosmic powers. Ask. Ask. Ask!”
I asked, “How can I use production and reliability statistics to:
- Increase production line throughput?
- Reduce the variance of throughput?
- Reduce the time from line startup to steady state production?”
“Aha!” The genie said, “You have to work on production lines now that products have become so reliable that reliability statisticians are no longer needed in design engineering.” Then the genie replied to all three wishes, “Increase the correlation between workstation times-between-failures (TBF) and subsequent times-to-repair (TTR) and between random processing times (PT) for the same solar tube at successive workstations.”
Astonished, I replied, “How do I do that? Those?”
Poof, the genie vanished, and I thought I heard him mutter, “Lousy statistician him. Three wishes, to be exact. And ixnay on the wishing for more wishes. That’s all. Three. Uno, dos, tres. No substitutions, exchanges or refunds.” [Robin Williams as the voice of the genie]
I rode home and verified the genie’s suggestion(s) with simulations that represent dependence. Then I searched for examples of production-line dependence. A pizza company improves production by reducing pizza crust variability. An engine-overhaul company mics the bores of engines before planning what to do to each engine. There’s also opportunistic maintenance…If it’s been a long time-between-failures, why not do more than just fix the symptom?
What would you do to increase the dependence of TBF and TTR and of workstation processing times, e.g., corr(TBF, TTR) and corr(PT(i),PT(j)?
Solyndra Solar Tube Production Lines
My objective was to simulate new solar-tube production-line alternatives to help optimize design, availability, throughput, and product quality. The new production line would use the same workstations and processes as the old production line, presumably with the same RAM statistics.
Production lines have workstations, buffers, and dependence within and between workstations. Data were observed workstation processing times and RAM data from the old production line: hourly production, TBFs, TTRs, maintenance and other downtimes, plus some solar-tube quality data.
Mechanics know that a short time-between-failures (TBF) often is followed by short time-to-repair (TTR) and vice-versa (long-long). Positive correlation of TBF and subsequent TTR reduces the variance of workstation availability, even though asymptotic availability remains MTBF/(MTBF+MTTR). Positive correlation also reduces the time to steady state. Bivariate lognormal TBF and TTR captured more dependence than alternative bivariate distribution models. Production line simulations also show that dependence reduces throughput uncertainty and time to converge to asymptotic throughput rate.
Exploit this result by increasing dependence. I.e., if it has been a long time between failures, then make longer repairs; if TBF is short, look for a quick fix. Perhaps the previous repair failed again? Consider opportunistic maintenance to combine repairs when workstations are unavailable [George and Lo].
“Models that use historical data too often apply distributions that are unrealistic” [Hubbard and Samuelson]. For example, simulated availability of the old solar-tube production line differed from observed availability, until dependence was included.
To evaluate production line alternatives and to quantify uncertainty, represent the dependence of time-between-failures (TBF) and subsequent time-to-repair (TTR). Multivariate normal and lognormal distributions are convenient, and, fortunately for this example, bivariate lognormal TBF and TTR fit better than alternatives and captured more dependence as evidenced by greater correlations. Weibull workstation TBFs and perhaps TTRs might have been convenient, if they fit data, because the minima of Weibull TBF random variables have the Weibull distribution too. That’s convenient for series production workstations when one workstation failure shuts down production or when all workstations are repaired at the same time. Use copulas to generate correlated Weibull TBF and TTR or other multivariate correlated distributions.
Production Line Simulation with Dependence for Portfolio Allocation
To evaluate production-line alternatives, I needed to simulate dependence in both RAM parameters and processing times to help allocate design and maintenance parameters [Meng and Yang]. Production line simulation software doesn’t represent dependence [McClain, Verma et al., Steiner and MacKay, Smith, Simsek and Fadiloglu, Hopp and Spearman]. Lack of data is no excuse for ignoring dependence. “89% of those surveyed used some subjective estimates…” “In 48% most of the inputs used were subjective estimates” [Hubbard and Samuelson]. So, if you don’t have enough data to quantify dependence, solicit subjective estimates of conditional distributions, P[TTF|TTR], and compute correlations from them [George and Mensing, https://accendoreliability.com/subjective-fragility-function-estimation/].
Availability formulas assume workstation independence and don’t represent uncertainty. Workstation availability A(t) is often approximated by the limit E[A(t)] as t→∞ equals MTBF/(MTBF+MTTR). However, asymptotic behavior depends on workstation MTBF, MTTR, VAR(TBF), VAR(TTR), and corr(TBF, TTR), but not on their distributions! In the limit as t→∞, Var[A(t)] is reduced by corr(TBF, TTR)>0 [Takacs]. A(t) arrives at limit sooner and with less variance when corr(TBF, TTR)>0.
Diffusion approximations to network of independent queues represent buffered production lines [George PhD Thesis]. Diffusion approximations could also be used to analyze dependent workstations in sequence, but I was getting paid by the hour, so I modified LineSim.xls [McClain] to include bivariate lognormal TBF and TTR dependent processing times. I simulated five replications of 24 hour runs for 22 full factorial design. Input factors were corr(lnTBF, lnTTR) and corr(lnPT(i),lnPT(j)) where PT(j) stands for workstation j processing time per product. Factor values were zero or observed correlations. Simulation computed average and standard deviations of hourly throughputs.
Average hourly throughputs were about the same with or without correlations. Throughput with independent TBF and TTR or independent processing times has more variance than when correlated positively. I.e., standard deviation of throughput decreases with dependence! I didn’t get around to optimization of buffer allocation [Allon et al.]. Optimization of workstation redundancy was not done because there was no redundancy.
Why care about variance of availability? Production-line reliability could be as important as product reliability!
I’ll try to explain why dependence reduces the asymptotic variance of workstation availability and throughput and reduces the time to steady state production. I didn’t get around to dealing with dependence of product quality on TBF and TTR, although I saw broken glass around workstations!
Variance reductions are due to a central limit theorem for renewal processes. The reduction of the time to steady state occurs because a smaller asymptotic variance is achieved sooner than a large asymptotic variance.
Managing a production line includes managing a portfolio of alternative improvement investments to: capital equipment and facilities, labor, service, spares, buffers, etc. Modern portfolio theory (MPT) [Markowitz] says, choose investment alternatives on the ”efficient frontier;” i.e., those alternatives with desired throughput (return) and the least variance of availability, or vice-versa, the alternatives with acceptable variance of availability and the greatest throughput. In the production-line context, quantify variance and risk to pick best alternative design availability with acceptably low variance.
How much should be spent on efficient-frontier alternatives, within budget? The Kelly criterion maximizes the utility from a series of bets. Kelly bets on efficient-frontier alternatives should be proportional to the budget multiplied by edge/odds or E[Throughput improvement]/Var[Throughput] for each alternative [Kelly, Thorpe].
What if there are too many alternatives, even using fractional Kelly bets, for your budget? MPT also says that a diversified portfolio will yield the same return as a single investment, with less variance, if some investment returns are negatively correlated [Markowitz]. In 2008 nearly all financial investment returns became positively correlated, reducing the value of MPT diversification. Reasonable production throughput improvements have positive correlations too. When the returns on investments are positively correlated, then the ”effective portfolio size” (the number of investments) is fewer than MPT would recommend.
Maximum throughput isn’t everything. Variance of throughput and reduced time to steady state should be considered too. Variance helps quantify risk, and risk reduction should be part of production line design and operation.
Availability and Throughput
Let X(t) = 1 indicate a workstation is up and 0 if down at time t. Availability definitions are:
- Point availability: A(t) = E[X(t)] = P[X(t) = 1]
- Interval availability: A(t) = ∫X(s)ds)/Δtime, where integral usually from 0 to Δtime.
A(t) is not MTBF/(MTBF+MTTR) for finite t unless TBF and TTR are independent exponentially distributed random variables and time starts at random within a cycle. Asymptotically A(t)→MTBF/(MTBF+MTTR) as time→∞ under conditions including:
- Up-down cycles constitute a renewal process,
- Nonlattice distributions, e.g., a workstation does not have deterministic TTF and TTR, and
- Asymptotic availability doesn’t depend on the distributions and dependence of TBF and TTR within cycles.
Throughput is availability times production rate. Some production line data showed that throughput variance was less than expected. Autocorrelation of workstation successive up-down cycle times was negligible, so up-down cycles constituted a renewal process. The correlation between TBF and subsequent TTR explained the decrease in throughput variance. Take advantage of that.
Variance of Up-Time and Availability
What is Var[Up-time(t)], the total up-time during calendar time t, as t→∞? Variances of availability and throughput can be computed from the variance of up-time. Normalized (standardized) up-time is asymptotically normally distributed as t→∞, regardless of interrival and service time distributions. Technically,
lim P[(Up-time(t)−M1t)/(M2√t) ≤ z] = Φ(z) as t→∞,
where M1 = MTBF/(MTBF+MTTR), M2 is its standard deviation, and Φ(z) is the cumulative standard normal distribution. The asymptotic variance of up-time is M22, [MTBF2Var(TTR)+MTTR2Var(TBF)]/(MTBF+MTTR)3.
This is from the central limit theorem for a renewal process that counts TBF-TTR cycles [Takacs],
lim P[(N(t)−λt)/(σ√λ3t) ≤ z] = Φ(z) as t→∞,
where N(t) is the number of renewals, with cycle times X, E[X] = 1/λ and σ is the standard deviation of X.
If TBF and subsequent TTR are dependent, then the asymptotic variance of up-time is
[MTBF2Var(TTR)+MTTR2Var(TBF)−2ρMTBFMTTR√(Var(TBF)Var(TTR)]/
(MTBF+MTTR)3,where ρ = corr(TBF, TTR).
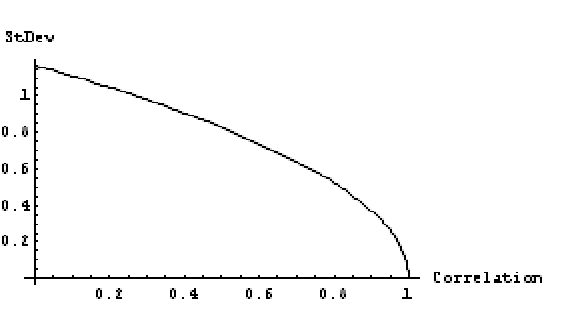
Figure 1 graphs up-time standard deviation M2 as a function of ρ for MTBF = 10, MTTR = 1, σ(TBF) = 5, σ(TTR) = 1. The vertical axis is the standard deviation of asymptotic up time, not availability itself, so the standard deviation can exceed 1. It makes sense that variance goes to zero as correlation goes to 1.0. Correlation of 1.0 implies that TTR is a linear function of TBF, so the the variance of up-time and also availability, Var[TBF/(TBF+TTR)], is zero.
Divide numerator and denominator of the first formula in this section by t to get the asymptotic availability,
P[Up-time(t)/t−M1)/(M2/√t) ≤ z] = P[A(t)−M1)/(M2/√t) ≤ z] = Φ(z).
Reduce Time to Steady State
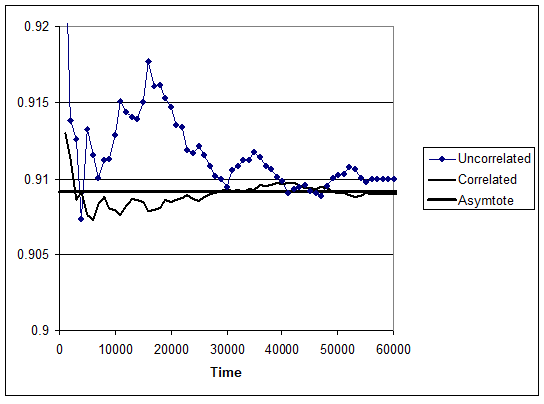
Figure 2 shows a workstation simulation for the MTBF =500, MTTR = 50, σ(TBF) = 100, σ(TTR) = 10, and correlation coefficient ρ = 0.9. TBF and TTR were normally distributed. The vertical axis is cumulative availability, up-time(t)/t. Other simulations show similar results. Regardless of correlation, workstation availability converges to 0.9091.
Steady state is subject to interpretation. If you agree that steady state is reached when the variance around asymptotic availability is small, then proof of the assertion practically unnecessary. This is because positive correlation of TBF and TTR reduces availability variance initially as well as asymptotically.
What’s the proof that positive correlation of TBF and TTR causes smaller variance of cycle availability, TBF/(TBF+TTR), not just asymptotically? Compute the distribution of cycle availability and its variance. Simulation is easier. Suppose only a single production cycle, one up-time and one down-time. I simulated 100 cycles ten times using the same distribution and parameters as in figure 2. The average of ten standard deviations with correlation of 0.9 was 0.007781, and without correlation it was 0.025128.
Recommendations and Extensions
Production lines provide opportunities to demonstrate reliability-related statistics. Encourage correlation of repair times with previous times between failures. The genie says workstation results apply to production lines too, surely for serial workstations [Dinçer and Deler, Hopp and Spearman] and probably for other production-line configurations. Simulations confirm the genie’s assertions. If you want proofs, use diffusion approximations to tandem queues [George PhD thesis].
Consider preventive maintenance and opportunistic maintenance; they will induce positive correlations, reduce variance of availability and throughput, and reduce the time to steady state. Relate product quality to workstation TTF and TTR parameters. Does product deteriorate waiting in buffers? Does it depend on workstation time since previous maintenance or adjustment? What if workstations contain redundancy? If the production line, serial or not, is Markovian or has regeneration times, the “functional” central limit theorem extends Takacs’ results for the entire line. Otherwise, simulate [Chovanec].
I am grateful to have had the Solyndra opportunity to work on their new production line. It was an opportunity to apply reliability statistics productively. Ask pstlarry@yahoo.com for help simulating and optimizing your production line. Send line description, workstation reliability and maintenance data, throughput or processing times, and product quality data. I’ll estimate multivariate distributions, simulate the line, compare with actual throughput, its variance, and product quality, and try to help make recommendations.
References
Chovanec, Alexej ”Prediction of the System Availability Using Simulation Modeling,” R&RATA Vol. 1, No. 4, https://studylib.net/doc/8822194/prediction-of-the-system-availability-using-simulation-mo…, Dec. 2008
Dinçer, C. and B. Deler “On the Distribution of Throughput of Transfer Lines,” J. Operational Research Society, Vol. 51, pp. 1170-1178, 2000
George, L. L. “Analysis of Two-Channel, Two-Queue Service Systems with Dependence,” UC Berkeley, Department of IE&OR, PhD thesis, 1973
George, L. L. and Yat H. Lo “An Opportunistic Look-Ahead Replacement Policy,” Spectrum, Society of Logistics Engineers, pp. 51-55, 1980
Hopp, Wallace J. and Mark L. Spearman “Throughput of a Constant WIP Manufacturing Line Subject to Failures,” Int. J. of Prod. Res., Vol. 29, No. 3, pp. 635-655, 1991
Hubbard, D., & Samuelson, D. A. “Modeling Without Measurements: How the decision analysis culture’s lack of empiricism reduces its effectiveness,” OR/MSToday, 36(5), 26–31, 2009
Kelly, J. L. Jr. “A New Interpretation of Information Rate”, Bell System Technical Journal, Vol. 35, pp. 917–926, http://en.wikipedia.org/wiki/Kelly_criterion, 1956
Markowitz, Harry “Portfolio Selection,” Journal of Finance, Vol. 7, No.1, pp. 77–91, http://en.wikipedia.org/wiki/Modern_portfolio_theory, 1952
Xiangsong Meng1 and Lixing Yang “Stochastic Portfolio Selection Problem with Reliability Criteria,” Discrete Dynamics in Nature and Society, Article ID 8417643, 11 pages http://dx.doi.org/10.1155/2016/8417643, 2016
McClain, John O. “LineSim.XLS A Serial Factory Simulator on a Microsoft Excel Spreadsheet,” Version 2.2, Feb. 1998
Simsek, Yasin and Murat Fadiloglu “Serial Production Line Simulator, A Performance Evaluation Tool,”
Smith, Jan Bryan “Method for assessing plant capacity,” US Patent 6334095, 2001, http://www.freepatentsonline.com/6334095.html
Steiner, Stefan H. and R. Jock MacKay “Teaching Variation Reduction Using a Virtual Manufacturing Environment,” The American Statistician, Vol. 63, No. 4, pp. 361-365, http://www.student.math.uwaterloo.ca/~stat435/login.htm, 2009
Takacs, Lajos ”Sojurn Time Problems,” The Annals of Probability, Vol. 2, No. 3, pp. 420-431, 1974
Thorp, E. O. ‘The Kelly criterion in blackjack, sports betting, and the stock market,” Handbook of Asset and Liability Management, Vol. 1, North-Holland, 2006
Verma, Rajesh, Ashu Gupta, and Kawaljeet Singh “Simulation Software Evaluation and Selection: A Comprehensive Framework,” J. Automation & Systems Engineering, Vol. 2, Issue 4, 14 p., Dec. 2008
Leave a Reply