In the 1960s, my ex-wife’s father set safety stock levels and order quantities for Pep Boys. He used part sales rates and the Wilson square-root formula to set order quantities.

Why not use the ages of the cars into which those parts go, to forecast part sales and recommend stock levels? Imagine you had vehicle counts (year, make, model, and engine) in the neighborhoods of parts stores, catalogs of which parts and how many go into which cars, and store sales by part number.
How do people forecast demand?
- Some inventory software says, “Please enter forecast______?” No kidding; I’ve seen it.
- A simple forecast is the demand rate (per unit installed per calendar interval) times the installed base (number of units at risk). [AFM23-120, AFMC Manual 20-106, Gaudette and Vinson, Dekker et al.]
- If people hate statistics and if they have enough lifetime data or products’ sales and spare parts consumption, they dump the data into artificial intelligence or machine learning software and extrapolate forecasts. [Posadas et al., Rosienkiewicz]
- Some statisticians make forecasts by extrapolating time series, without regard to products’ installed base or its ages. “Smart” forecasters use tournaments to select best time-series-extrapolation model [e.g., Willemain, Smart, and Schwarz; https://smartcorp.com/smartforecasts-demand-planning-forecasting/, Levenbach]. In 1991, Apple Computer forecast tournaments results were boring; the tournament winner was the same model for nearly every data set.
- Actuarial forecasts based on installed base, its ages, and reliability
I learned actuarial methods while working on gas turbine engine maintenance for the US Air Force Logistics Command [AFLCM 66-7, AFM 400-1, Campbell]. Gas turbine engines and major modules are tracked by serial number, flying hours, and cycles, so it’s easy to estimate actuarial rates from lifetime data. Actuarial rates are discrete, conditional probabilities: either a(t) =P[t<age at failure≤t+Δt|Life > t] for product or part failures or d(t) = P[t<Product age at event≤t+Δt|Product Life > t] for recurrent events such as part replacements or service events.
An actuarial forecast is an estimate of expected or average demand, Σa(t-s)*n(s) or Σd(t-s)*n(s), s=1,2,…,t, where n(s) is the installed base of age s and a(t-s) or d(t-s) is the actuarial (age-dependent) failure or demand rate. (The usual numbering of installed base means n(1) is the oldest cohort from period 1.) Actuarial forecasts are more accurate and precise than demand rate times installed base, because they account for installed base of different ages with age-dependent actuarial rates.
I figured out how to estimate age-dependent actuarial rates from ships and returns counts, data required by Generally Accepted Accounting Principles [Plank]. I am still trying to persuade the USAF, RAND, and DLA to use actuarial methods for all service parts, not just those tracked by serial number.
I admit that automotive aftermarket parts stores do NOT keep track of the vehicle a part’s sale is intended for. The company I worked for bought vehicle registration counts by zip code and year, make, model, and engine. Part of my job was to partition the zip codes nearest to parts stores.

Dwight Jennings “DJ” (Aug. 25, 1947-Feb. 7, 2022) gave me Apple Computer service parts’ monthly returns counts. Apple required service providers to return failed parts in order for them to purchase replacements. I got bills-of-materials for all of Apple’s computers to count how many service parts were in each computer. I had to look up Apple computer sales in industry publications. Those computer ships and parts returns counts were statistically sufficient data to make nonparametric estimates of all Apple Computer service parts’ reliability functions and actuarial failure rates and to recommend spares stock levels based on service providers’ computer sales.
When Apple service providers saw the stock level recommendations, they screamed! They had been stuck with buying obsolescent spares. I asked how required stock levels had been determined. The answer was, “We guessed.” Apple put me in charge of buying back $36M of obsolescent spare parts and spreading the charge over three calendar quarters. DJ and I collaborated on reliability estimates long after I quit Apple.
Actuarial demand forecasts for Apple computer service parts were more accurate and precise than time-series extrapolations, because actuarial forecasts use the service parts’ actuarial demand rates based on computers’ ages. Service parts’ demands are driven by the age and usage of the products the parts go into. Why not use products’ ages and bills of materials that tell which parts and how many go into each system?
What is Installed base?
It helps if you know how many products you’re supporting and how old they are [Dekker et al., do Regoa and de Mesquita, Murty]. When I was estimating the reliability of Firestone tires, Ford incendiary ignition switches, and 1988 Ford 460 cubic-inch-displacement (cid) engines, I got Ford’s installed base from industry publications. When I sent reliability estimates to Ford friends, they sent back the actual monthly vehicle sales.
If you don’t track parts’ lives by name and serial number, you still need parts’ installed base to estimate their field reliability. How many service parts go into your products’ installed base? How old are the parts? GOZINTO theory tells how many parts there are in those products by the ages of the products the parts go into [https://accendoreliability.com/gozinto-theory-parts-installed-base/#more-417514].
What if same replacement or service can happen more than once?
1988 Ford V8 460 cid engines were notorious for requiring repeated service. They were the last carbureted engines Ford made. They didn’t need spare parts, just service adjustments. Dwight Jennings owned one and sold it when warranty expired! [https://accendoreliability.com/renewal-process-estimation-without-life-data/] Other products consume spare parts repeatedly; helicopters have been described as service parts flying in close formations.
Product ships (installed base by age) and parts’ returns, replacements, or service counts are statistically sufficient to make nonparametric estimates of actuarial (age-specific) demand rates. The actuarial forecast for repairable or replaceable parts or for repeated service events is described in https://accendoreliability.com/please-enter-forecast_____/.
What is the probability distribution of demand?
Please distinguish between the expected value of demand (forecast) and the probability distribution of demand (prediction). Demand is a random variable, and a forecast is typically an estimate of the expected value of the demand random variable. Demand is the sum of demands from cohorts of different ages, ΣD(s;t) s=1,2,…,t, where each D(s;t) is the demand from installed base n(s) (except for attrition and prior failures) of age s times the actuarial failure rate for age a(t-s). The actuarial forecast Σn(s)*a(t-s) is an estimate of expected demand. The demand random variable is the sum of n(s)*A(t-s) terms where actuarial rate A(t-s) is random because it is an estimate. Future installed base may also be random.
For inventory decisions and risk analyses, the probability distribution of demand in some future time interval is needed to manage backorders and recommend spares stock levels to satisfy fill rate or service level preferences.
Sources of uncertainty should be accounted for in the probability distribution, actuarial rates, and demand forecasts:
- Sample uncertainty occurs if your life data or ships and returns counts are a sample of the population. For example, the automotive aftermarket company I worked for sampled 2000 aftermarket auto parts stores. That was a convenience sample determined by how much money the company could make selling information and software back to the parts stores.
- Future or model uncertainty: occurs even though the actuarial demand rate estimates may have come from population data and consequently have no sample uncertainty. There is uncertainty about what the future demand rates will be. Assuming the demand process remains stationary, then classical asymptotic statistics of maximum likelihood (Cramer-Rao [Janssen]) or least squares estimators (martingale central limit theorem) apply. Both lead to asymptotic multivariate normal distributions for actuarial rate estimates and for actuarial forecasts.
- The future installed base must be estimated, and actuarial rates must be extrapolated for the oldest units in the installed base in the future forecast time interval. I use subset regression and prediction limits to extrapolate and quantify extrapolation uncertainty. Attrition should be quantified and included too.
I didn’t quantify the sample uncertainty (source 1) in automotive aftermarket demand forecasts, because I had no information about how the sample of aftermarket parts’ stores was selected. I assumed actuarial demand forecasts were the mean rates of Poisson processes for recommending spares stock levels. This is the same as US Air Force Logistics Command assumed for engines 50 years ago [George 20004, AFLCM 67-1, AFM 400-1]. If the automotive aftermarket company had not been bought in a leveraged buyout, I would have tried to quantify the sample uncertainty induced by the 2000-store sample with the bootstrap [Efron, https://en.wikipedia.org/wiki/Bootstrapping_(statistics)/, Cowling et al.]. I did that for COVID-19 forecasts, and I would do that for quantifying future uncertainty.
Bootstrap demand variance
In addition to making a demand forecast, at least estimate demand variance, which depends on the variance of actuarial rate estimates AND their covariances. The variance of demand is the variance of a sum, Σn(s)*A(t-s) =
Σn(s)2*Var[A(t-s)]+2ΣΣn(r)*n(s)*COV[A(t-r),A(t-s)] r<s = 1,2,…,t, where A(t-s) actuarial rate estimates are dependent random estimates.
The table 1 data are COVID-19 case and death counts from early in the pandemic. COVID-19 was not a recurrent event in 2020, but I used the bootstrap to quantify variance of actuarial death forecasts. Bootstrap simulates death counts from a nonparametric estimate of the survival function, P[Death date-Case date > t], because case cohort counts are known. A VBA program simulated bootstrap deaths from each cohort and from the survival function estimate. Another VBA program makes maximum likelihood estimates of survival functions and actuarial rates from the simulated deaths. Future installed base in the forecast interval was extrapolated using regression; actuarial rates from all observed and simulated actuarial rates were also extrapolated.
Table 1 is the original data and the maximum likelihood estimates of the survival function G(t) and actuarial rates a(t). The survival function was constant for periods 7-15, and the corresponding actuarial rates were zero.
| Period t | Cases | Deaths | Survival function G(t) | Actuarial rate a(t) |
| 1 | 5 | 0 | 0 | 0 |
| 2 | 23 | 1 | 0.0255 | 0.0255 |
| 3 | 78 | 2 | 0.0255 | 0 |
| 4 | 252 | 6 | 0.0255 | 0 |
| 5 | 442 | 13 | 0.0294 | 0.004 |
| 6 | 398 | 17 | 0.0342 | 0.0049 |
| Etc. | Etc. | Etc. | Etc. | Etc. |
Table 2 Shows the statistics of the original and bootstrap simulated actuarial rate estimates. The skew and kurtosis indicate non-normal distribution. All 20 simulated actuarial rates a(1) were zero.
| Period t | Original | Mean | Median | Var | Skew | Kurtosis |
| 1 | 0 | 0.0000 | 0.0000 | 0.00E+00 | #DIV/0! | #DIV/0! |
| 2 | 0.0255 | 0.0020 | 0.0000 | 2.12E-05 | 2.2566 | 3.8661 |
| 3 | 0 | 0.0044 | 0.0000 | 3.61E-05 | 0.9905 | -0.3720 |
| 4 | 0 | 0.0048 | 0.0028 | 3.55E-05 | 1.0046 | -0.3081 |
| 5 | 0.004 | 0.0056 | 0.0037 | 3.41E-05 | 0.7172 | -0.7175 |
| 6 | 0.0049 | 0.0110 | 0.0119 | 4.48E-05 | -0.4282 | -0.8012 |
The skew and kurtosis (table 2) of the actuarial rate estimates do not support the assumption of normal distributions, although they should have asymptotic multivariate normal distributions according to the Cramer-Rao inequality (maximum likelihood estimates) or the martingale central limit theorem (least squares estimates).
The bootstrap didn’t work! The simulated death counts didn’t match the observed death counts, nor did the original actuarial rates (column B table 2) resemble the simulated actuarial rate means (column C table 2). The least squares and maximum likelihood survival function estimated disagreed. Figure 1 shows the maximum likelihood and least squares estimates of the cumulative distributions function (cdf) of duration from case to death for all data. The least squares cdf estimate found an apparent increase. Simulated deaths from the least squares cdf estimate were biased way too large. I should have checked whether the deaths process was stationary; i.e., whether the survival functions from each cohort were the same!

Figure 1. Cumulative distribution function estimates by maximum likelihood (MLE G(t)) and least squares (LSE G(t)).
The table 1 data set was not stationary: different cohorts had different survival functions. Figure 2 is a “broom” chart (Jerry Ackaret) shows the stochastic process of cases and deaths was nonstationary. A broom chart is a graph of cdf, reliability, or survival function estimates: from first two periods, first three periods, etc. to all periods, the longest line. The broom chart shows steadily decreasing cdf (maximum likelihood) estimates as subsets added more recent periods. I should have checked for stationarity. I hope my next data set behaves better. Don’t do as I do; check your data for nonstationarity before assuming all cohorts have same reliability. (Another story for another time. SELInc EPROMS made by Catalyst Semiconductor lost their little memories after Catalyst Semi. Shrunk the die size.)
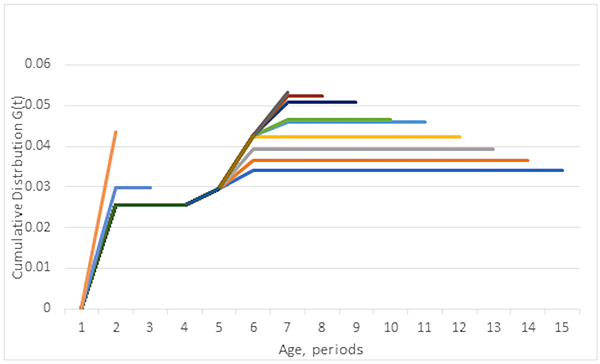
Figure 2 is a “Broom” chart of cumulative distribution function (survival function) estimates from successively earlier subsets of cases and deaths. Shorter lines are from earlier data, longer lines include more periods, and the lowest, blue line is from all 15 periods of data. The pattern of decreasing as lines get longer indicates nonstationarity and improvement in treatment or changes in data reporting.
Pay Attention. This is new!
To bootstrap simulated samples of a nonstationary process without life data, I needed the reliability function estimates from each cohort, NOT the broom chart estimates from cohort subsets from periods 1 and 2, periods 1, 2, and 3, etc. So I made spreadsheets for maximum likelihood and least squares cdf estimates from each cohort.
The least squares estimate minimizes the sum of squared errors (SSE) between observed deaths and hindcast deaths, sums from each period. Hindcasts are actuarial forecasts of each periods’ deaths as functions of actuarial rates, with different actuarial rates for each cohort. Sums of hindcasts from each cohort are estimates of period deaths, from cohort from period 1, periods 1 and 2, periods 1, 2, and 3, etc. Excel Solver finds the actuarial rates that minimized the SSE.
The figure 3 maximum likelihood estimates use the facts that each period’s cohort outputs (deaths) could be modeled as Poisson outputs of an M(t)/G(s)/Infinity self-service system that has nonstationary Poisson input distribution (M(t)) and the sum of independent Poisson processes is also Poisson. I wrote formulas for the Poisson likelihood of deaths in each period in terms of the times-to-deaths from each cohort. I used Excel Solver iteratively to find maximum likelihood estimates of the probability distributions G(s;t) for each cohort s=1,2,…,15. (Solver allows no more than 200 variables, and the maximization involved 225 variables. So I reran Solver on different subsets: periods and ages.)

Figure 3. Maximum likelihood cumulative distribution function estimates by cohort
The nearly vertical cdf estimate is from period 1, the oldest cohort, with only 5 cases. It is an outlier but doesn’t affect simulations much. All cdf estimates are for G(s,t) for t=1,2,…,15, even though cohorts from periods 3,4,…,15 did not contribute deaths of ages 15, 14,…,2 respectively. That’s the magic of maximum likelihood; it maximized the probability of what you observed using the variables I varied, G(s,t) for t=1,2,…,15, using all the information in observations.
I wrote a VBA code to simulate deaths from each cohort using each cohort’s estimated cdf. Then I made actuarial forecasts for period 16 by extrapolating cases and actuarial rates. (The simulated forecasts from the least-squares survival function estimates were biased too large. The same happened for simulated deaths from the least squares cdf in figure 1.)
Table 4. Hindcasts and simulated forecasts for period 16, from 9 simulated bootstrap death counts. Column “Observed” is reported deaths, and columns “Simulate” are bootstrap deaths.
| Period t | Cases | Observed | Simulate | Simulate | Simulate | Simulate |
| 1 | 5 | 0 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 23 | 1 | 0.13 | 0.00 | 0.00 | 0.00 |
| 3 | 78 | 2 | 0.59 | 0.12 | 0.05 | 0.03 |
| 4 | 252 | 6 | 1.99 | 0.54 | 0.21 | 0.15 |
| 5 | 442 | 13 | 6.45 | 1.82 | 0.71 | 0.51 |
| 6 | 398 | 17 | 11.39 | 5.92 | 2.38 | 1.74 |
| Etc. | ||||||
| 16 | 1105 | 33.936 | 33.94 | 28.11 | 20.08 | 19.34 |
The averages of the period 16 forecasts from simulated samples differ from the demand formula standard deviation computed from the original data and actuarial rates because of bias in the bootstrap simulation. I verified this by simulating 20 samples from a simulated returns count from a stationary process using the G(t) distribution estimated from all of the original ships and one set simulated returns. The simulated sample of 20 gave unbiased returns counts and reproduced the G(t) distribution used to simulate them.
Table 5. Variance-covariance matrix of bootstrap actuarial rate estimates, COVAR[a(s),a(t)]. Most covariances were zero because covariance with a sample of constants is zero. Variances are on the diagonal.
| s/t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 0.0E+00 | |||||||
| 2 | 0.0E+00 | 0.0E+00 | ||||||
| 3 | 0.0E+00 | 0.0E+00 | 0.0E+00 | |||||
| 4 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 0.0E+00 | ||||
| 5 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 0.0E+00 | |||
| 6 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 4.7E-10 | ||
| 7 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 0.0E+00 | -5.7E-06 | 2.1E-11 | |
| 8 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 0.0E+00 | 0.0E+00 | -9.9E-06 | 2.8E-07 | 9.0E-11 |
Table 6. Parameters of period 16 forecasts vs. computed forecast parameters from 9 simulated case counts
| Average | Median | Stdev | |
| Sample | 21.10 | 21.34 | 0.67 |
| Formula | 1.0045 |
The sample standard deviation of the simulated period 16 forecasts is less than the standard deviation computed from the formula that includes the covariances of the actuarial rates. The simulated forecasts variances (Sample) are less that computed from the variance-covariance formula (Formula), because the simulated forecasts are of the expected demand, not the variance of the demand random variable! The variance of a random variable’s expected-value estimate is not usually the same as the variance of a random variable. If you want to recommend stock levels, you need the demand distribution, not average demand! If normally distributed, mean and variance-covariance estimates are all you need to characterize the distribution of actuarial rate estimators.
More work!
There is no sample uncertainty in demand forecasts from population data, except for extrapolated installed base and actuarial rates. Model uncertainty comes from the concern whether the future demand process remains statistically similar to the past (stationarity) and from how representative the past data is of the demand process. I modified the bootstrap to deal with the nonstationary demand process.
Regression extrapolation effect on demand distribution may be subject of a future article. Extrapolation of installed base depends on possible attrition [Dekker et al.], on the regression model, and on the subset of actuarial rates the regression is applied to! If you send data, explain it, and ask for forecasts, I will provide demand forecasts and their variance estimates.
References
AFLCM 66-17, ““Quantitative Analyses, Forecasting, and Integrative Management Techniques for Maintenance Planning and Control,” U.S. Air Force Logistics Command, Wright-Patterson AFB, Ohio, March 27, 1970, revised June 20, 1973
AFM 400-1, “Logistics, Selective Management of Propulsion Units, Policy and Guidance,” U.S. Air Force, June 21, 1976
AFM23-120, “Spares Requirement Review Board (SRRB),” Nov. 2019
AFMC Manual 20-106, “Provisioning,” Dec. 2018
H. S. Campbell “Procurement and Management of Spares,” The RAND Corporation, 1966
Ann Cowling, Peter Hall, and Michael J. Phillips, “Bootstrap Confidence Regions for the Intensity of a Poisson Point Process,” Journal of the American Statistical Association, Vol. 91, No. 436, pp. 1516-1524, Dec., 1996
Rommert Dekker, Çerağ Pinçe, Rob Zuidwijk, and Muhammad Naiman Jalil, “On the use of installed base information for spare parts logistics: A review of ideas and industry practice,” International Journal of Production Economics, Volume 143, Issue 2, pp. 536-545, June 2013
Kevin Gaudette and Jason Vinson, “Customer-oriented leveling technique: COLT uses a marginal analysis technique to achieve the best possible objective while satisfying constraints,” Air Force Journal of Logistics, Supply 2003
George, L. L., https://accendoreliability.com/gozinto-theory-parts-installed-base/#more-417514
George, L. L., https://accendoreliability.com/renewal-process-estimation-without-life-data/
George, L., “Actuarial Forecasts for the Automotive Aftermarket,” SAE Technical Paper 2004-01-1538, https://doi.org/10.4271/2004-01-1538, 2004
Catherine Huber “Robust and Non Parametric Approaches to Survival Data Analysis,” https://link.springer.com/chapter/10.1007/978-0-8176-4924-1_21, 2010
Arnold Janssen “A nonparametric Cramer–Rao inequality for estimators of statistical functionals, Statistics & Probability Letters 64 pp. 347-358, 2003
Hans Levenbach, Four Peas in a Pod, e-Commerce Forecasting and Planning for Supply Chain Practitioners, Amazon, Aug. 2021
Katta G. Murty “Forecasting for Supply Chain and Portfolio Management,” Univ. of Michigan, Nov. 2006
Katta G. Murty, “Use of Installed Base Information for Spare Parts Logistics: a Review of Ideas and Industry Practice,” Report Econometric Institute EI201073, 2010
Tom M. Plank, Accounting Deskbook, 10th Edition, New York, Prentice-Hall, 1995
Sergio Posadas, Carl M. Kruger, Catherine M. Beazley, Russell S. Salley, John A. Stephenson, Esther C. Thron, and Justin D. Ward. “Forecasting Parts Demand Using Service Data and Machine Learning,” Volume 1, LMI, Jan. 2020
José Roberto do Regoa and Marco Aurélio de Mesquita “Spare parts inventory control: a literature review,” Produção, v. 21, n. 4, out./dez, pp. 656-666, doi: 10.1590/S0103-65132011005000002, 2011
Maria Rosienkiewicz, “Artificial Intelligence Methods in Spare Parts Demand Forecasting,” https://www.researchgate.net/publication/298203927, January 2013
Thomas R. Willemain, Charles N. Smart, and Henry F. Schwarz, “A new approach to forecasting intermittent demand for service parts inventories”, International Journal of Forecasting, 20, 375–387, 2004
Leave a Reply